| Zufallszahlengeneratoren mit Gamma und Mersenne Twister - Standardnormal- und Gammaverteilung |
 |
 |
 |
| Geschrieben von: Kristian | |||||
| Sonntag, den 18. November 2007 um 10:10 Uhr | |||||
Seite 2 von 3
StandardnormalverteilungDie behandelte allgemeine Gaußsche Normalverteilung lässt sich mit den speziellen Parameterwerten μ = 0 und σ = 1 auf die so genannte Standardnormalverteilung N(0; 1) zurückführen. Der Übergang wird durch Substitution erreicht. Die Fläche der Dichtefunktion nimmt dabei den Wert 1 an. Die Dichtefunktion der Standardnormalverteilung lautet, wie folgt: 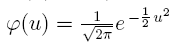 Die zugehörige Verteilungsfunktion lautet:  Das Integral hat keine elementare Lösung, aber es existieren viele gute Approximationen die auf numerische Integration zurückgreifen. Der meistverwendete Algorithmus ist Algorithmus 26.2.17 im Nachschlagewerk von Abromowitz und Stegun, Handbuch der Mathematischen Funktionen. Er hat einen maximalen absoluten Fehler von 7.5e^-8. Die Implementierung ist in der nächsten Zeile dargestellt. double N(const double x) { const double b1 = 0.319381530; const double b2 = -0.356563782; const double b3 = 1.781477937; const double b4 = -1.821255978; const double b5 = 1.330274429; const double p = 0.2316419; const double c = 0.39894228; if(x >= 0.0) { double t = 1.0 / ( 1.0 + p * x ); return (1.0 - c * exp( -x * x / 2.0 ) * t * ( t *( t * ( t * ( t * b5 + b4 ) + b3 ) + b2 ) + b1 )); } else { double t = 1.0 / ( 1.0 - p * x ); return ( c * exp( -x * x / 2.0 ) * t * ( t *( t * ( t * ( t * b5 + b4 ) + b3 ) + b2 ) + b1 )); } } Bevor wir uns mit einer vollständigen Implementierung der Standardnormalverteilung in C++ befassen, möchten wir anhand eines Beispiels, ein klassisches Einsatzgebiet der Gaußschen Normalverteilung aufzeigen. Dazu eignet sich die Betrachtung der Auswertung eines Intelligenztests sehr gut. Wenn man einen Intelligenztest an einer repräsentativen Stichprobe normiert, unterstellt man häufig eine Normalverteilung der Testpunkte, die die Untersuchungspersonen bei dem Test erzielen. Die Testrohwerte werden für jede Altersgruppe so transformiert, dass sich ein durchschnittlicher Punktwert von 100 und eine Standardabweichung von 15 ergibt. Nach dieser Normierung kann der Test für diagnostische Zwecke verwendet werden. Wenn beispielsweise eine Person, deren Intelligenz diagnostiziert werden soll, insgesamt 113 Testpunkte erzielt, betrachtet man die Wahrscheinlichkeit, ein solches Testergebnis zu erreichen, um zu beurteilen, wie überdurchschnittlich intelligent die Person ist. In dem Beispiel geht es also um die Wahrscheinlichkeit, maximal einen Punktwert von X = 113 zu erreichen, wenn die Verteilung aller Punktwerte einer Normalverteilung folgt, durchschnittlich einen Wert von μ = 100 Punkten aufweist und die Varianz aller Punktwerte σ² = 15² = 225 beträgt. In unserem Beispiel erzeugen wir Zufallszahlen entsprechend der Standardnormalverteilung, die innerhalb der Standardabweichung σ = 1 liegen. Wir greifen dazu auf die seit 1958 bekannte Box-Muller Transformation zurück. Für den Fall das wir eine Gleichung haben, die unsere gewünschte Verteilungsfunktion beschreibt, ist es möglich einen mathematischen Trick anzuwenden, der auf den fundamentalen Transformationsgesetzen für Wahrscheinlichkeiten beruht, um an eine transformierte Funktion für die Verteilung zu gelangen. Die Transformation nimmt zufällige Variablen aus einer beliebigen Verteilung entgegen und generiert zufällige Variablen in einer neuen Verteilungsfunktion. Das erlaubt uns einheitlich verteilte Werte in einen neuen Satz normalverteilter Zufallszahlen zu transformieren. Die gängigste Form der Transformation sieht wie folgt aus: y1 = sqrt(-2 * ln(r1)) * cos(2 * PI * r2) y2 = sqrt(-2 * ln(r1)) * sin(2 * PI * r2) Wir starten mit zwei unabhängigen Zufallszahlen, r1 und r2, welche von einer einheitlichen Verteilungsfunktion stammen (zwischen 0 und 1). Die dafür notwendige C-Funktion haben wir bereits auf der ersten Seite kennengelernt. Anschließend wenden wir die obige Transformation an um zwei unabhängige Zufallszahlen zu erzeugen die innerhalb der Standardnormalverteilung liegen, also die speziellen Parameterwerte μ = 0 und σ = 1 aufweisen. #include <iostream> #include <cstdlib> #include <cmath> #include <ctime> #include <iterator> #include <algorithm> double const PI = 4 * std::atan(1.0); // Functor for normal distribution class normal_distribution { public: normal_distribution(double m, double s) : mu(m), sigma(s) { } double operator()() { // Generates a equal distribution in the range [0, 1] double r1 = (std::rand() + 1.0) / (RAND_MAX + 1.0); double r2 = (std::rand() + 1.0) / (RAND_MAX + 1.0); return mu + sigma * std::sqrt(-2 * std::log(r1)) * std::cos(2 * PI * r2); } private: double mu, sigma; }; int main() { double samples[100]; srand((unsigned)time(NULL)); // Assigns the normal distributed values generated by a function object to a // specified number of element in a range and returns to the position // one past the last assigned value. std::generate_n(samples, 100, normal_distribution(1.0, 0.5)); std::copy(samples, samples + 100, std::ostream_iterator<double>(std::cout, "\n")); return 0; } Diese besondere Transformation hat aber zwei entscheidende Nachteile.
Das sind ernsthafte Probleme falls sie stochastische Modellierungen durchführen oder Millionen von Zufallszahlen generieren wollen. Die Polarform der Box-Muller Transformation ist schneller und robuster. Der Algorithmus ist folgendermaßen definiert: #include <cmath> extern float ranf(); // ranf() is uniform in 0..1 // mean m, standard deviation s float box_muller(float m, float s) { float x1, x2, w, y1; static float y2; static int use_last = 0; if (use_last) { y1 = y2; use_last = 0; } else { do { x1 = 2.0 * ranf() - 1.0; x2 = 2.0 * ranf() - 1.0; w = x1 * x1 + x2 * x2; } while (w >= 1.0); w = sqrt((-2.0 * log(w)) / w); y1 = x1 * w; y2 = x2 * w; use_last = 1; } return m + y1 * s; } Die Funktion ranf() steht provisorisch für einheitlich verteilte Zufallszahlen im Bereich zwischen 0 und 1. Es existieren neben den benannten Algorithmus noch weitere, wie der von Graeme West. Dabei handelt es sich um einen hochpräzisen (double) Algorithmus der im Artikel Better Approximations to Cumulative Normal Fuctions näher beschrieben wird. Der Algorithmus basiert auf Hart's Algorithmus 5666 aus dem Jahre 1968. Wir wollen nicht näher auf diesen Algorithmus eingehen, da dieser bereits ausführlich in dem Dokument beschrieben wird. Die GammaverteilungWir haben uns nun mit der grundlegensten kontinuierlichen Wahrscheinlichkeitsverteilung, der Gaußschen Normalverteilung befasst und Methoden kennengelernt statistisch normalverteilte Zufallszahlen mit dem Rechner zu generieren. Die Art und Weise, wie unsere Zufallszahlen generiert worden sind, hat uns dabei allerdings nicht interessiert. Genauer gesagt haben wir in fast allen Fällen die allseits bekannte Funktion rand() für die Erzeugung der Zahlen verwendet. Bevor wir uns im konkreten Fall mit bekannten Algorithmen aus Pseudozufallszahlengeneratoren beschäftigen, möchten wir uns noch mit einer letzten, aber wichtigen Wahrscheinlichkeitsverteilung auseinander setzen, der Gammaverteilung. Die Gammaverteilung ist ebenfalls eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie ist definiert über der Menge der positiven reellen Zahlen. Einerseits ist die Gammaverteilung eine direkte Verallgemeinerung der Exponentialverteilung und andererseits eine Verallgemeinerung der Erlang-Verteilung für nichtganzzahlige Parameter. Sie findet unter anderem Anwendung in der Warteschlangentheorie, um die Bedienzeiten oder Reparaturzeiten zu beschreiben und in der Versicherungsmathematik zur Modellierung kleinerer bis mittlerer Schäden. Die allgemeine Dichtefunktion der Gammaverteilung kann in Bezug auf die Gammafunktion folgendermaßen ausgedrückt werden: 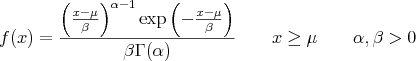 Der Parameter α bezeichnet den sogenannten Formparameter, μ die Lokalisierung und β den Skalenparameter. Die Gammaverteilung leitet sich aus der Gammafunktion ab, die wie folgt definiert ist: 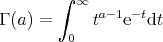 Nachfolgend sehen sie ein Java-Applet das die Gammaverteilung in Abhängigkeit des Formparameters und des Skalenparameters darstellt. Dabei ist zu beachten das der Formparameter mit δ abgekürzt wurde und der Skalenparameter als Inverse λ = 1 / β definiert ist. Diese Art der Parametrisierung wird sehr oft verwendet. Ähnlich zu der Standardnormalverteilung mit N(0; 1) sehen wir uns bei der Gammaverteilung den Fall μ = 0 und β = 1 etwas näher an. Wir erhalten mit diesen Parametern die folgende Dichtefunktion: 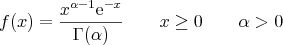 Damit lässt sich ein Graph generieren, der die Verteilung von Zufallszahlen grafisch veranschaulicht. Dazu werden 1000 Zufallszahlen aus zwei unterschiedlichen Sequenzen generiert. Jedes Paar an Zahlen wird gegeneinander geplottet, um das Verhalten der Gammaverteilung bei diesem, nicht gleich verteilten, Zufallszahlengenerator zu demonstrieren.  Gamma-verteilte Zufallsvariablen eignen sich zur Modellierung von Prozessen, bei denen es um Wartezeiten zwischen ”zufälligen“ Ereignissen geht. In der Eisenbahnbetriebswissenschaft sind dies zum Beispiel Ankünfte der Züge an bestimmten Stellen im Eisenbahnnetz, oder aber die zeitliche Verteilung der Wunschtrassen bei der Trassenvergabe in der Fahrplanerstellung. Die weitgehend freie Wahl der Parameter bietet einen großen Spielraum bei der Beschreibung von stochastischen Vorgängen. Wir wenden uns nun von kontinuierlichen Wahrscheinlichkeitsverteilungen für Zufallszahlen ab und gehen über zu den Algorithmen die von gängigen Zufallszahlengeneratoren verwendet werden um diese Zahlen zu generieren. Im nächsten Abschnitt gehen wir auf den Mersenne-Twister Pseudozufallszahlengenerator ein. |
|||||
| Zuletzt aktualisiert am Montag, den 23. April 2012 um 00:27 Uhr |
| AUSWAHLMENÜ | ||||||||
|
 Wir suchen ständig neue Tutorials und Artikel! Habt ihr selbst schonmal einen Artikel verfasst und seid bereit dieses Wissen mit der Community zu teilen? Oder würdet ihr gerne einmal über ein Thema schreiben das euch besonders auf dem Herzen liegt? Dann habt ihr nun die Gelegenheit eure Arbeit zu veröffentlichen und den Ruhm dafür zu ernten. Schreibt uns einfach eine Nachricht mit dem Betreff „Community Articles“ und helft mit das Angebot an guten Artikeln zu vergrößern. Als Autor werdet ihr für den internen Bereich freigeschaltet und könnt dort eurer literarischen Ader freien Lauf lassen.
Wir suchen ständig neue Tutorials und Artikel! Habt ihr selbst schonmal einen Artikel verfasst und seid bereit dieses Wissen mit der Community zu teilen? Oder würdet ihr gerne einmal über ein Thema schreiben das euch besonders auf dem Herzen liegt? Dann habt ihr nun die Gelegenheit eure Arbeit zu veröffentlichen und den Ruhm dafür zu ernten. Schreibt uns einfach eine Nachricht mit dem Betreff „Community Articles“ und helft mit das Angebot an guten Artikeln zu vergrößern. Als Autor werdet ihr für den internen Bereich freigeschaltet und könnt dort eurer literarischen Ader freien Lauf lassen.
