| Künstliche neuronale Netze in C# |
 |
 |
| Geschrieben von: Kristian, Alex | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Samstag, den 23. Juli 2011 um 20:00 Uhr | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Inhaltsverzeichnis
VorspannIn diesem Artikel werden künstliche neuronale Netze (kurz: KNN) aus der der Neuroinformatik vorgestellt. Basierend auf den theoretischen Grundlagen wird eine C#-Bibliothek für KNN entwickelt. Die Originalbibliothek enthält neben den hier vorgestellten Algorithmen auch genetische Algorithmen und selbstorganisierende Karten (engl. self-organizing map). Der Artikel zeigt wie künstliche neuronale Netze zur Mustererkennung und allgemein zum maschinellen Lernen genutzt werden können. Auf Basis der Programmbibliothek wird eine Anwendung zur Handschrifterkennung entworfen, um das Konzept vorzustellen. Einführend soll auf die Fähigkeiten und Eigenschaften künstlicher neuronaler Netze eingegangen werden. EinleitungComputer können in der Regel viele Aufgaben deutlich schneller durchführen als wir Menschen. Doch bedeutet schneller nicht immer besser. Es existieren viele Aufgaben in denen Computer ihrem menschlichen Gegenüber unterlegen sind. Vorschulkinder sind bereits in der Lage zwei unterschiedliche Bilder mit einem Hund und einer Katze auseinanderzuhalten, während sich diese augenscheinlich triviale Aufgabe für einen Computer auch heutzutage noch als beachtliche Herausforderung herausstellt. Sehr viele Tätigkeiten im täglichen Leben kann der Mensch schnell und erfolgreich erledigen ohne lange darüber Nachdenken zu müssen. Das Halten des Gleichgewichtes beim Gehen oder das Erkennen von Gesichtern gehört beispielsweise dazu. Der Begriff „Nachdenken“ geht über das bloße Denken hinaus und beschreibt dabei eine Ereignisabfolge, nämlich dass Aussagen unter der Nutzung von Schlussfolgerungen logisch zu neuen Gedanken, neuen Aussagen verknüpft werden. Ein komplexer Algorithmus zur Lösung einer Aufgabe ist eine aus endlich vielen Schritten bestehende eindeutige Handlungsvorschrift zur Lösung eines Problems, die in aller Regel exakt durchdacht werden muss. Das Laufen vollzieht sich hingegen unterbewusst. An dieser Stelle kann auch keine Verarbeitung von Regeln stattfinden, da eine Regelverkettung zu viel Zeit beanspruchen würde. Viele Fähigkeiten des Menschen beruhen auf antrainierten Verhaltensweisen, die ohne Nachdenken angewendet werden. Die meisten dieser antrainierten Fähigkeiten können auch relativ schnell auf neue, noch nie vorher in genau dieser Weise aufgetretene Situationen angewendet werden. Hunde unterscheiden sich äußerlich voneinander, dennoch kann ein Mensch ein Objekt auch dann noch als Hund identifizieren, wenn er die Rasse noch nie zuvor gesehen hat. In der Regel benötigt er dafür nur die Bruchteile einer Sekunde. Eine biologische Nervenzelle hat eine Schaltzeit von etwa einer Millisekunde, so dass der gesamte Prozess in etwa 100 Schritten abgeschlossen wird. Im Vergleich zu einem modernen Mikroprozessor, der in einer Millisekunde mehrere Millionen Maschineninstruktionen abarbeiten kann ist diese Zeit dennoch sehr hoch. Dieser Nachteil wird allerdings dadurch kompensiert dass das Gehirn hochgradig parallel arbeitet. Moderne Computer können die für den Menschen scheinbar einfach ablaufenden Prozesse bisher nur sehr schwer oder überhaupt nicht nachbilden. Ein Themenschwerpunkt ist die Bilderkennung bei Robotern, die in einer natürlichen Umgebung operieren müssen. An diese Stelle treten künstliche neuronale Netzwerke, kurz: KNN (engl. artificial neural network – ANN). Neuronale Netze sind ein Forschungsgebiet der künstlichen Intelligenz und versuchen die Arbeitsweise des menschlichen Gehirns nachzubilden. Ähnlich wie beim menschlichen Gehirn sollen Computer in Zukunft in die Lage versetzt werden mithilfe von Training bestimmte Steuerungsaufgaben durchzuführen und Erlerntes auf neue Situationen anzuwenden. Das soll Probleme lösen, die sich bisher auf dem Computer als schwierig umsetzbar erwiesen haben. Existiert keine algorithmische bzw. regelbasierte Lösung, könnte ein neuronales Netzwerk in Zukunft zum Einsatz kommen. Da das Gehirn als gesamtes Konstrukt zu komplex ist, um es auf einem Computer zu modellieren, werden in erster Linie die biologischen Nervenzellen, auch Neuronen genannt, studiert. Neuronen sind spezialisierte Zellen und bilden die Grundlage für den menschlichen Denkprozess. In diesem Artikel soll ein KNN in C# entwickelt werden, das auf dem Prinzip vorwärts gerichteter neuronaler Netze basiert. Das künstliche NeuronDas biologische Vorbild von künstlichen neuronalen Netzwerken ist die biologische Nervenzelle. In künstlichen neuronalen Netzwerken bildet das künstliche Neuron die Basis für das Modell der künstlichen neuronalen Netze.  Die Dendriten der biologischen Nervenzelle nehmen die Erregungen, die von anderen Neuronen ausgehen, auf und leiten sie an den Zellkern weiter. Die Erregung der Zelle wird anschließend über das Axon an die nächsten Neuronen weitergeleitet. Neuronen stellen die Verbindung über chemische Botenstoffe und Neurotransmitter her. Die Axonterminale werden von anderen Neuronen durch eine Kontaktstelle, die Synapse, getrennt. Die Synapsen stellen den Übergang vom Axon der einen Zelle zu den Dendriten weiterer Zellen her. Ein biologisches Neuron hat mehrere tausend bis zehntausend Verbindungen zu weiteren Neuronen. Das künstliche Neuron als Modell kann mehrere Eingaben verarbeiten und entsprechend über seine Aktivierung reagieren. Dazu werden die Eingaben gewichtet an eine Ausgabefunktion übergeben, welche die Neuronenaktivierung berechnet. Der Grundaufbau wird in Form von Softwarebausteinen nachgebildet.  Der Baustein für ein künstliches Neuron besteht aus mehreren Werten und Funktionen. Das Neuron selbst ist eine Verarbeitungseinheit, die die über gewichteten Verbindungen (engl. weight) eingehenden Werte geeignet zusammenfasst (Propagierungsfunktion) und daraus mithilfe der Aktivierungsfunktion aj über einen Schwellwert (engl. threshold) einen Aktivierungszustand ermittelt. Aus der Aktivierung bestimmt eine Ausgabefunktion oj die Ausgabe des Neurons. EingabeinformationenDen Beginn bilden die Eingabeinformationen ok aus den gewichteten Verbindungen wkj, die andere Neuronen mit dem Neuron j besitzen, oder die direkt aus der Umgebung des Netzes als Eingabewerte aus der Umgebung auf das Neuron einfließen. PropagierungsfunktionDen zweiten Schritt bildet die Propagierungsfunktion netj, die alle Eingabeinformationen mit den Gewichten der Verbindungen zu einer einzigen Netzeingabe verknüpft. Die Netzeingabe stellt die Summe aller Informationen dar, die aus dem Netz an das Neuron weitergegeben werden. AktivierungsfunktionDer wesentliche Aspekt innerhalb von biologischen und künstlichen Neuronen liegt in der Aktivierungsfunktion. Biologische Neuronen arbeiten analog, d.h. sie können auf kontinuierliche Schrittfolgen reagieren. Moderne Computer sind digitale Rechenmaschinen mit nur zwei Zuständen, 0 oder 1. Künstliche Neuronen müssen deshalb analoge Schwellwertfunktionen nachbilden. Dies geschieht in der Aktivierungsfunktion. Der Aktivierungszustand aj eines Neurons wird in der technischen Realisierung unterschiedlich dargestellt. Man unterscheidet (quasi-) kontinuierliche und diskrete Wertebereiche. Im Falle kontinuierlicher Wertebereiche unterscheidet man wiederum Modelle, die alle reellen Zahlen (real, double) als Werte zulassen, andere verwenden ein Intervall. Die meisten Modelle beschränken die Aktivierung auf ein Intervall, beispielsweise [0, 1] oder [−1, 1]. Dies kommt daher, dass diese Modelle meistens eine nichtlineare, häufig sigmoide Aktivierungsfunktion mit S-förmigen Graphen und die Identität als Ausgabefunktion verwenden, wodurch die Ausgabe identisch mit der Aktivierung wird und der Wertebereich der Aktivierungsfunktion den Wertebereich des Aktivierungszustandes angibt.  Bekannte Aktivierungsfunktionen sind die lineare Funktion, auch Identität genannt oder eine binäre Schwellwertfunktion. Bei der linearen, wenig sigmoiden Funktion wird die Netzeingabe direkt weitergereicht. Die Schwellwertfunktion ist hingegen die schärfste sigmoide Funktion. Erst wenn die Netzeingabe den Schwellwert θ des Neurons überschreitet, wird das Neuron aktiviert.   Einige Lernverfahren erwarten differenzierbare Aktivierungsfunktionen mit stetig ändernden Werten, so dass oftmals auch logistische Funktionen und hyperbolische Tangens-Funktion zum Einsatz kommen. Es handelt sich dabei um sogenannte Sigmoidfunktionen oder S-Funktion mit einem S-förmigen Graphen.  Über den Parameter c wird in der sigmoiden, logistischen Funktion die Steilheit der Kurve gesteuert.  AusgabefunktionAm Ende jedes Neurons steht die Ausgabefunktion. Sie kommt, wie bereits erwähnt, fast ausschließlich als Identität zum Einsatz. Ist das der Fall, kann die Aktivierung des Neurons gleichzeitig auch als Ausgabe betrachtet werden. Bei der Kodierung der Ausgabewerte ist bei der sigmoiden Funktion zu beachten, dass die Ausgabewerte 0 und 1 nie erreicht werden können, da die Funktion zwei horizontale Asymptoten besitzt. Um Ausgangswerte zu erhalten, die nahe 0 bzw. 1 liegen, ist betragsmäßig ein hoher Nettoinput erforderlich und somit auch sehr hohe Gewichte. Das kann zu Laufzeitfehlern führen. Daher sollten die Ausgabewerte auf ein kleineres Intervall, wie z.B. [0.1; 0.9], abgebildet werden. Linear Threashold UnitDas einfachste künstliche neuronale Netzwerk besteht nur aus einem Neuron. Ein derartiges Gebilde wird Linear Threashold Unit genannt, kurz LTU. Um eine logische UND-Verknüpfung nachzubilden müssen lediglich geeignete Gewichte und Schwellwerte gefunden werden. Dies kann bei einfachen Modellen direkt geschehen oder im Training erlernt werden.  Es existieren zwei Eingaben. Da der Schwellwert bei 1,5 liegt, feuert das Neuron erst dann, wenn beide Eingänge aktiv sind. NetzwerkarchitekturenNeuronale Netzwerke bestehen in der Regel aus zahlreichen Neuronen, da erst in der Summe die besonderen Eigenschaften von neuronalen Netzen emergieren. Ein neuronales Netz besteht immer aus einer Menge von Neuronen, die durch gerichtete und gewichtete Verbindungen miteinander verknüpft sind. Durch die Menge an Verbindungen werden unterschiedliche Architekturen definiert. Üblicherweise wird das Verbindungsnetzwerk der Neuronen in einer Matrixschreibweise angegeben. Die Verbindungsgewichte lassen sich zusammen mit den Verbindungen dann jederzeit angeben. Anhand der Matrix-Muster lässt sich auch schnell herauslesen um welche Art von Netzwerk es sich handelt.
 In dem mehrstufigen vorwärts gerichteten Netz, wird neben der Eingabeschicht und der Ausgabeschicht noch eine verdeckte Schicht von Neuronen eingefügt. Zu der verdeckten Schicht gehören die Neuronen 3, 4, 5 und 6. Die Matrix zeigt in dem Beispiel nur Verbindungen ohne konkrete Gewichte auf. Die Netztopologie von neuronalen Netzwerken wird in zwei Kategorien unterteilt, Netze ohne Rückkopplung (engl. feedforward) und Netze mit Rückkopplungen. Bei Netzen ohne Rückkopplung existiert kein Pfad, der von einem Neuron direkt oder über zwischengeschaltete Neuronen wieder zu dem Neuron zurückführt. Zwischengeschaltete Neuronen können auch mittels „shortcut connection“ übersprungen werden. Mathematisch ist die Topologie eines Netzes ohne Rückkopplung ein azyklischer Graph. In dem oben vorgestellten Beispiel ist deshalb nur die obere Dreiecksmatrix mit einem Rechteck gefüllt. Netze mit Rückkopplungen unterteilt man meistens in die Klassen der Netze mit direkten Rückkopplungen (engl. direct feedback), Netze mit indirekten Rückkopplungen (engl. indirect feedback) und Netze mit Rückkopplungen innerhalb einer Schicht (engl. lateral feedback) und vollständig verbundene Netze. Netze mit direkten Rückkopplungen ermöglichen es, dass ein Neuron seine eigene Aktivierung über eine Verbindung von seinem Ausgang zu seinem Eingang verstärkt oder abschwächt. Diese Verbindungen bewirken oft, dass Neuronen die Grenzzustände ihrer Aktivierungen annehmen, weil sie sich selbst verstärken oder hemmen können. Innerhalb der Netze mit indirekten Rückkopplungen gibt es eine Rückkopplung von Neuronen höherer Ebenen zu Neuronen niederer Ebenen. Diese Art der Rückkopplung ist nötig, wenn eine Aufmerksamkeitssteuerung auf bestimmte Bereiche von Eingabeneuronen oder auf bestimmte Eingabemerkmale durch das Netz erreicht werden soll. Netze mit Rückkopplungen innerhalb derselben Schicht werden oft für Aufgaben eingesetzt, bei denen nur ein Neuron in einer Gruppe von Neuronen aktiv werden soll. Jedes Neuron erhält dann hemmende (inhibitorische) Verbindungen zu anderen Neuronen und oft noch eine erregende (exzitatorische) direkte Rückkopplung von sich selbst. Das Neuron mit der stärksten Aktivierung (der Gewinner) hemmt dann die anderen Neuronen, daher heißt eine solche Topologie auch „The Winner takes it all“ -Netzwerk. Die vollvernetzten Schichten haben Verbindungen zwischen allen Neuronen und sind bekannt als Hopfield-Netze. Das folgende Beispiel zeigt ein weiteres Netz samt Matrix. Es handelt sich um ein Netz mit indirekten Rückkopplungen, in dem das siebte Neuron zurück auf die Neuronen 3, 4 und 5 verweist.
 Hopfield-NetzeEin neuronales Hopfield-Netz ist wahrscheinlich das einfachste Netzwerk, mit mehr als einem Neuron. Es bezeichnet eine besondere Form eines künstlichen nicht trainierbaren neuronalen Netzes. Hopfield-Netze gehören zur Klasse der vollvernetzten Netze mit Rückkopplung. Jedes der binären Neuronen ist mit jedem, ausgenommen sich selbst, verbunden. Bei einem Hopfield-Netz existiert nur eine Schicht, die gleichzeitig als Ein- und Ausgabeschicht fungiert. Das Netz ist ein Autoassoziationsnetz, d.h. es gibt das Eingabemuster exakt wieder.  Matrix mit Verbindungsgewichten entwerfenIn dem folgenden Beispiel wird ein Verfahren vorgestellt mit dem die Verbindungsgewichte für ein vorgegebenes Muster ermittelt werden. Das dargestellte Hopfield-Netz soll das Binärmuster 0101 erkennen können.  Um das Netz manuell zu trainieren, muss eine Akzeptanzmatrix für das Muster 0101 hinzugefügt werden. Die Berechnung von Akzeptanzmatrizen für Hopfield-Netze kann in drei Schritten erfolgen. Im ersten Schritt wird eine bipolare Darstellung des Binärmusters berechnet, da die 0 mathematisch nicht die Inverse von 1 ist. Um die Umwandlung vorzunehmen, kann folgende Funktion verwendet werden.  Daraus ergibt sich das bipolare Muster -1, 1, -1, 1. Die mehrzeilige Matrix wird nun mit ihrer Transponierten multipliziert. 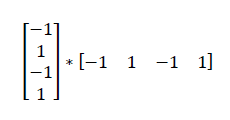 Das Ergebnis der Matrizenmultiplikation ist die folgende Matrix.  Da die Neuronen in einem Hopfield-Netz keine direkte Rückkopplung auf sich selbst aufweisen, wird abschließend die Diagonale durch eine Subtraktionen mit der Einheitsmatrix bzw. Identitätsmatrix eliminiert.  Das dargestellte Ergebnis ist die endgültige Akzeptanzmatrix für das Muster 0101. Hopfield-Netze haben die Eigenschaft für antrainierte Akzeptanzmatrizen auch stets das Einerkomplement zu akzeptieren. Mit der berechneten Matrix kann ein Hopfield-Netz also auch das Muster 1010 erkennen. Wie lernt die MaschineEs gibt viele unterschiedliche Wege, wie ein neuronales Netzwerk lernt. Die meisten Lernprozesse verändern die Matrix mit den Verbindungsgewichten. Für den Lernprozess spielt die Struktur des künstlichen neuronalen Netzes eine Rolle. Neuronale Netze lassen sich nach unterschiedlichen Kriterien unterteilen. Bevor der eigentliche Lernprozess beginnen kann, muss ein neuronales Netz in seiner Struktur entwickelt werden. Die Entwicklung von neuronalen Netzwerken verläuft in mehreren Zyklen. Da es keine allgemeine Erfolgsstrategie für die Entwicklung neuronaler Netzwerke gibt, lässt sich eine Lösung meist nur mittels vieler Experimente erreichen. Ausgehend von dem zu lösenden Problem ist zuerst die Netzwerkarchitektur aufzubauen. Mithilfe von Trainingsdaten wird ermittelt, ob das Netz geeignet ist. Anschließende Testdaten geben Auskunft über die Generalisierungsfähigkeit des Netzes, d.h. wie das Netz auf bisher unbekannte Eingaben reagiert. Sind die Ergebnisse noch nicht zufriedenstellend, müssen die Netzparameter verändert werden. Die Modifikation kann die Lernparameter, als auch den Lernalgorithmus oder die Netzwerkarchitektur betreffen.  Welche Probleme eignen sich?Neuronale Netze eignen sich nicht für Probleme die direkt aus Flussdiagrammen abgeleitet werden können. Wenn alle Schritte zur Lösung des Problems im Detail bekannt sind, können diese in der Regel direkt in einer Programmiersprache implementiert werden. Ein weiterer Aspekt von neuronalen Netzen ist die Fähigkeit zu lernen. Algorithmen die sich nicht mehr verändern, sind für neuronale Netze uninteressant. Konkret hat der Lernprozess allerdings zur Folge das die exakte Lösung mithilfe von neuronalen Netzen nicht bekannt ist. Das KNN kann keine Auskunft darüber geben, wie es zu der Lösung gelangt ist. Aus diesem Grunde eignen sich künstliche neuronale Netzwerke besonders gut für Probleme, die nicht mit eindeutigen Schritten ausgedrückt werden können. Dazu zählt beispielsweise die Mustererkennung, die sequentielle Vorhersage oder das sogenannte Data Mining. Ein KNN ist besonders gut geeignet für Probleme, die sich stetig verändern und deren Lösung eine Anpassung verlangt. LernmethodenDie Lernmethoden bzw. -verfahren beschreiben das Training in einem Netz. Das Training ist ein elementarer Vorgang innerhalb von neuronalen Netzen. Man unterteilt die Lernmethoden in ein überwachtes (engl. supervised) und ein nicht überwachtes (engl. unsupervised) Lernen. Überwachtes LernenBeim überwachten Lernen gibt es zu jedem Eingabemuster der Trainingsmenge das korrekte bzw. beste Ausgabemuster. Dem neuronalen Netz liegt damit immer gleichzeitig ein vollständig spezifiziertes Eingabemuster und das korrekte bzw. optimale, vollständig spezifizierte Ausgabemuster für diese Eingabe vor. Entdeckte Fehler werden zum „Lernen“, genauer gesagt zum Verändern der Verbindungsgewichte sowie der Schwellwerte in den Neuronen benutzt. Es existieren viele unterschiedliche überwachte Lernalgorithmen. Die Backpropagation-Lernverfahren sind bekannte Vertreter. Genetische Algorithmen werden ebenfalls häufig verwendet. Künstliche neuronale Netze mit überwachtem Lernen sind weniger häufig vertreten und haben kein biologisches Vorbild. .png) Das dargestellte Flussdiagramm stellt den Ablauf beim überwachten Lernen vor. Die Berechnung der Fehlerrate ist ein wesentliches Merkmal bei dieser Lernmethode. Nicht überwachtes LernenDas nicht überwachte Lernen ist biologisch plausibler. Das Netz „merkt“ selbst, wie es auf die Ausgaben zu reagieren hat. Nicht überwachtes Lernen wird immer dann angewendet, wenn das Ergebnis nicht bekannt ist. Anwendungen sind beispielsweise Clusterungen beim Data Mining, das sind Klassifizierungsversuche, wobei Art und Umfang der Klasseneinteilung vorher nicht bekannt sind. .png) Nicht überwachte Lernmethoden sind oftmals bei selbstorganisierenden Karten, sogenannten Kohonenkarten oder Kohonennetzen zu finden. Bestärkendes LernenBeim bestärkenden Lernen wird nicht die erwünschte Ausgabe angegeben, sondern nur, ob die Ausgabe richtig oder falsch ist, eventuell noch der Grad der Richtigkeit. Jedoch sind keine Zielwerte für die einzelnen Ausgabeneuronen vorhanden. Das Lernverfahren muss selbst die richtige Ausgabe dieser Neuronen finden. Diese Art Lernverfahren sind neurobiologisch bzw. evolutionär plausibler, weil man einfache Rückkopplungsmechanismen der Umwelt (Bestrafung bei falschen Entscheidungen, Belohnung richtigen) bei niederen und höheren Lebewesen beobachten kann. LernregelDie Lernregel ist die mit Abstand interessanteste Komponente von Modellen neuronaler Netze, weil sie es gestattet, dass ein Netz eine gegebene Aufgabe (weitgehend) selbständig aus Beispielen lernt. Dazu muss eine Lernregel existieren. Es existieren gibt es sehr viele Arten, wie ein neuronales Netz lernen kann. Allen neuronalen Netzen ist es dabei gemeinsam, dass eine Vielzahl einfacher Einheiten, Neuronen oder Teilchen, zusammen eine Aufgabe zu lösen haben. Die Lernregel verfolgt dabei nicht das Ziel eine Lösung durch einen Algorithmus explizit zu beschreiben, sondern deren Lösung durch Beispiele zu beschreiben. Ziel einer Lernregel ist es das Netz zu beeinflussen, durch
Die Entwicklung neuer Zellen oder das Absterben von nicht genutzten Neuronen ist das biologische Gehirn angelehnt. Diese Methode, die neben einer Einstellung der Gewichte gleichzeitig eine (möglichst) optimale Topologie des Netzes liefern soll findet zunehmend Verwendung bei dem Entwurf von KNN. In der Regel werden allerdings primär nur die Gewichte zwischen den neuronalen Verbindungen modifiziert. Hebbsche LernregelEine der bekanntesten Lernregeln ist die Hebbsche Lernregel. Die Regel wurde von Donald Olding Hebb formuliert um das nicht überwachte Lernen zu unterstützen. Sie ist die älteste und einfachste neuronale Lernregel. Die Hebbsche Lernregel besagt das wenn Zelle j eine Eingabe von Zelle i erhält und beide gleichzeitig stark aktiviert sind, dann erhöhe das Gewicht wi, j (die Stärke der Verbindung von i nach j). Dabei ist Δwi,j die Änderung des Gewichts wi,j, η die Lernrate (ein konstanter Faktor), oj die Ausgabe von Neuron i und aj die Aktivierung von Neuron j. Die Hebbsche Lernregel wird häufig bei binären Aktivierungswerten verwendet. Dabei muss man aber beachten, dass sich in diesem Fall nur positive Gewichtsänderungen oder Null ergeben können, wodurch die Gewichte nur monoton steigen können, jedoch nicht mehr verringert werden können. Oftmals verwendet man deshalb die binären Aktivierungen -1 und 1 anstelle von 0 und 1, so dass die Hebbsche Regel eine Verringerung der Gewichte bewirkt, wenn das Vorgängerneuron und das Nachfolgerneuron nicht übereinstimmen, sonst eine positive Verstärkung. Delta-RegelDie Delta-Regel ist auch unter dem Begriff LMS-Algorithmus (Least-Mean-Squares-Algorithmus) bekannt. Es handelt sich um ein Verfahren zur Adaption der Gewichte innerhalb eines vorwärtsgerichteten Netzes mit nur einer Schicht von trainierbaren Verbindungen. Bei der Delta-Regel ist die Gewichtsänderung proportional zur Differenz δj der aktuellen Aktivierung aj und der erwarteten Aktivierung tj (teaching input). Die mathematisch verallgemeinerte Formel für die Delta-Regel lautet: In dem nachfolgenden Beispiel wird als Fehler die Differenz zwischen erwarteter Ausgabe für ein bestimmtes Eingabemuster und der vom Netz tatsächlich berechneten Ausgabe betrachtet. Der Ausgabewert (teaching output) tritt an die Stelle der Aktivierung. Zusätzlich wird eine Lernrate gewählt, die unter dem Schwellenwert liegen sollte. Mit der Lernrate wird gesteuert, wie stark ein Fehler bei der Korrektur der Gewichte berücksichtigt wird. Ohne Lernrate würden die Gewichte oszillieren, ohne das ein Lernen im Sinne einer Konvergenz der Gewichtswerte stattfinden würde.  An die UND-Funktion wird das Eingabemuster x1 = (o1, o2) = (1, 1) angelegt. Die LTU berechnet dann die Ausgabe o: Mit dem Ergebnis der Ausgabe, kann der Fehler als Abweichung δj der Eingabe x1 von der erwarteten Ausgabe, dem teaching output tj berechnet werden. Bei einer UND-Funktion wird als Ausgabe eine 1 erwartet, somit beträgt der Fehler 1. Der Fehler wird nun zur Korrektur der Verbindungsgewichte verwendet. Durch Multiplikation des Fehlers mit dem Ausgabewert wird erreicht, dass nur Gewichte verändert werden, über deren Verknüpfung ein Betrag zum Fehler zustande kam. Als Lernrate η wird der Faktor 0.2 gewählt. Analog zu der Rechnung ergibt sich für die neue Gewichtung von w2 der Wert 0.2. Wird der Vorgang nun für weitere Eingabemuster wiederholt, so ergibt sich folgendes Resultat.
Für die korrekte Erkennung aller Muster ist eine Runde erforderlich. Nachdem die Gewichte den Wert 0.4 erreicht haben, funktioniert die UND-Funktion für alle Eingabemuster richtig. Theoretisch wäre bereits ein Wert von 0.25 dank des Schwellenwertes von 0.5 ausreichend, um korrekte Ergebnisse zu gewährleisten. Mit einer entsprechend kleineren Lernrate η ist dies zu realisieren, hat aber zur Folge, dass mehr Lernschritte notwendig sind, bis die Werte konvergieren. Wird ein Lernwert höher als der Schwellwert gewählt, kann die Delta-Regel die Schrittfolge der Gewichte nicht mehr ausreichend feingranular anpassen und die Gewichte beginnen zwischen den Runden zu oszillieren. Backpropagation-RegelDie Backpropagation-Regel ist eine Verallgemeinerung der bereits vorgestellten Delta-Regel für Netze mit mehr als einer Schicht trainierbarer Gewichte und für Neuronen mit einer nichtlinearen Aktivierungsfunktion. Die Aktivierungsfunktion muss semilinear, d.h. monoton und differenzierbar, sein. Der Unterschied zur Delta-Regel besteht darin, dass die Berechnung der δj komplizierter ist. Die Formel des Backpropagation-Verfahrens wird durch Differentiation hergeleitet. Die Rückwärtspropagierung ist ein Spezialfall eines allgemeinen Gradientenabstiegsverfahrens in der Optimierung, basierend auf dem mittleren quadratischen Fehler. Wenn man den Fehler eines neuronalen Netzes als Funktion der Gewichte des Netzwerks graphisch aufträgt, erhält man eine Fehlerfläche, die sich im zweidimensionalen Fall anschaulich graphisch darstellen lässt.  In der Abbildung wird eine mögliche Fehlerkurve E(w1, w2) für zwei Gewichte dargestellt. Gesucht werden Gewichte, so dass die Fehlerkurve ein globales Minimum einnimmt. Um in ein Tal der Fehlerfunktion zu gelangen, müssen die Gewichte geeignet verändert werden. Bei mehrdimensionalen Kurven ist der Gradient von E an der Stelle (w1, w2) ein Vektor in der w1-w2-Ebene, der in die Richtung des steilsten Anstiegs von E an dieser Stelle zeigt und dessen Länge ein Maß für die Steilheit (Steigung) ist. Leitet man eine mehrstellige Funktion partiell nach einer Variablen ab, so entspricht dies einer Projektion des Gradienten auf die Richtung dieser Variablen. Die partielle erste Ableitung der Fehlerfunktion nach einer Gewichtsvariablen kann für die Korrektur dieses Gewichtes verwendet werden.  Die Lernrate γ bestimmt den Grad der Änderung. Das negative Vorzeichen kennzeichnet die Veränderung entgegen dem Kurvenanstieg in Richtung Fehlertal. Die Art der Fehlerkurve ergibt sich aus dem gewählten Trainingsmuster. Jede Ausgabe eines Neurons wird mittels der Ausgabefunktion aus der Aktivierung eines Neurons bestimmt. Die Aktivierung lässt sich durch Anwendung der Aktivierungsfunktion auf die Netzeingabe berechnen. Diese ist ihrerseits von den Werten der Verbindungsgewichte abhängig. Daraus ergibt sich der Zusammenhang zwischen Fehler und Gewicht.  Der Fehler ist abhängig vom Ausgabewert, der Ausgabewert ist abhängig von der Netzeingabe und diese wiederum ist abhängig von dem einzelnen Gewicht. Die gesamte Netzeingabe ist von den Verbindungsgewichten und der Netzeingabe selbst abhängig. Nach der Differentiation entfallen alle Summanden bis auf k = i.  Die Abhängigkeit der Ausgabe von der Netzeingabe ist durch die Aktivierungsfunktion vorgegeben, sofern die Identität verwendet wird.  Da lineare Netze nur lineare Funktionen berechnen können und mehrstufige Netze mächtiger sind als einstufige Netze, sind Trainingsverfahren für mehrstufige nichtlineare Netze notwendig. Für die angepasste Delta-Regel wird eine nichtlineare Aktivierungsfunktionen gewählt. Oftmals wird die differenzierbare logistische Aktivierungsfunktion verwendet. Daraus ergibt sich dann: .png) Der Fehler kann nur für ein Ausgabe-Neuron direkt als Differenz zwischen dem Trainingswert tj und der berechneten Ausgabe oj ausgedrückt werden.  Um zu verhindern das sich positive und negative Abweichungen gegenseitig aufheben, wird die Differenz quadriert. Der Faktor ½ wurde verwendet, damit er sich später gegen eine 2 weg kürzt, die durch das Differenzieren entsteht. Damit kann nun die dritte partielle Ableitung bestimmt werden. .png) Für ein inneres Neuron wird der Fehler aus den Fehlersignalen den nachfolgenden Neuronen ermittelt. .png) Daraus ergibt sich die allgemeine Formel für das Fehlersignal. .png) Zu beachten ist, dass hierbei der Summationsindex k über alle direkten Nachfolge-Neuronen des aktuellen Neurons j läuft. Dies erkennt man auch an der Indizierung des Gewichts wjk. Mit den häufig verwendeten Funktionen bei Backpropagation, der Standard-Propagierungsfunktion, der logistischen Aktivierungsfunktion und der Identität als Ausgabefunktion ergibt sich für das Fehlersignal δj. .png) Um ein Fehlersignal eines Neurons in der inneren Schicht anhand der Fehlersignale aller nachfolgenden Neuronen berechnen zu können, muss zunächst das Fehlersignal der Ausgabe-Neuronen bestimmt werden. Der Fehler wird von der Ausgabeschicht zur ersten inneren Schicht zurück „propagiert“, was dem Algorithmus den Namen Backpropagation verliehen hat. MomentumUm die Konvergenz des Backpropagation-Lernverfahrens zu beschleunigen, werden in der Praxis einige Anpassungen beim Lernverfahren vorgenommen. Ein bekanntes Verfahren wird nachfolgend vorgestellt.  Wenn das Minimum der Fehlerfunktion für eine vorgegebene Lernphase innerhalb eines eng begrenzten “Tals” liegt, kann das Folgen der Gradientenrichtung zu umfangreichen Oszillationen beim Suchvorgang führen. In der Abbildung wird ein Netzwerk mit nur zwei Gewichten w1 and w2 dargestellt, einmal ohne und einmal mit Momentum. Die beste Strategie liegt darin, die Suche in Richtung globales Minimum, also in Richtung Tal, auszurichten. Allerdings ist die Form der Fehlerfunktion derart, dass der Gradient nicht kontinuierlich in diese Richtung zeigt. Eine einfache Möglichkeit korrigierend einzugreifen bietet die Einführung eines weiteren Parameters, da so genannte Momentum. Der Gradient der Fehlerfunktion wird für jede neue Kombination von Gewichten berechnet. Anstatt aber nur der negativen Gradientenrichtung zu folgen, wird ein gewichteter Mittelwert von der aktuellen und vorherigen Gradientenrichtung bei jedem Schritt ermittelt. Theoretisch verleiht dieser Ansatz dem Suchverfahren eine gewisse Trägheit und hilft dabei exzessive Oszillationen in schmalen Minima der Fehlerfunktion zu verhindern. Wie in dem Kapitel zuvor dargestellt, wird im Backpropagation-Lernverfahren ein Eingabe/Ausgabe-Muster an das Netz gelegt und die Fehlerfunktion E am Ausgang bestimmt. Wenn das Backpropagation-Lernverfahren zusammen mit einem Momentum in einem Netzwerk mit n verschiedenen Gewichten w1, w2, . . . ,wn verwendet wird, wird die i-te Korrektur für ein Gewicht wk durch die folgende Formel beschrieben.  Die Lernrate wird mit γ (griech. gamma) und das Momentum mit α (griech. alpha) bezeichnet. Im Normalfall ist man daran interessiert die Geschwindigkeit der Konvergenz zu einem Minimum der Fehlerfunktion zu erhöhen und das kann dadurch erreicht werden, dass man die Lernrate auf einen optimalen Wert erhöht. Das Momentum dämpft die Oszillationsrate der Iterationen. Die Anpassung beider Parameter erfolgt normalerweise durch Versuch und Irrtum. Grenzen des BackpropagationDie Festlegung des Lernparameters γ hat einen großen Einfluss auf die Qualität des Backpropagation-Lernverfahrens. Die Lernrate wird in der Regel zwischen 0 und 1 festgelegt, in Ausnahmefällen kann dieser Wert aber auch höher sein. Für die optimale Wahl existieren keine Regeln, da der Parameter in Abhängigkeit von der Problemstellung, den Trainingsdaten sowie der Topologie und der Netzdimensionierung zu wählen ist. Ein weiteres Aspekt ist die Wahl der Initialisierungsgewichte, die die Konvergenz des Lernverfahrens bestimmen. Sind die Initialisierungsgewichte zu groß, so ergibt die Ableitung der sigmoiden Aktivierungsfunktion einen Wert nahe 0. Sind die Gewichte jedoch sehr klein gewählt, so liegt der Nettoinput der inneren und äußeren Neuronen nahe 0. Beides verlangsamt das Lernverfahren. Es ist deshalb üblich den Initialisierungsgewichten Werte aus festen Intervallen, wie z.B. [-1; 1] oder [-0.5; 0.5], zuzuweisen. Dabei muss allerdings darauf geachtet werden, dass nicht alle Gewichte des Netzes mit dem gleichen Wert initialisiert werden, da dies zu einer symmetrischen Weiterentwicklung der Gewichtsveränderungen führen würde. Alle Gewichte eines Eingabe-Neurons i zu den verdeckten Neuronen j sind in jeder Phase des Trainings gleich. Ebenso entsteht für die Gewichte der inneren Neuronen zu einem Ausgabe-Neuron eine Symmetrie, die nicht mehr durchbrochen werden kann. Dies führt meist dazu, dass mit dem Netz keine Lösung mehr erreicht wird. Die Initialisierung der Gewichte hat damit eine wesentliche Bedeutung und muss mehrmals mit einer Zufallszahl vorgenommen werden. Gradientenorientierte Verfahren, wie das Backpropagation-Lernverfahren, konvergieren immer, können allerdings lokale Optima nur schlecht überspringen. Backpropagation kann das globale Minimum nicht immer bestimmen, da häufig mehrere lokale Minima existieren und der Optimierungsverlauf von der Anfangsinitialisierung abhängt. Für die Optimierung neuronaler Netze bietet es sich an, genetische Algorithmen mit einem gradientenorientierten Lernverfahren zu koppeln, wodurch die Nachteile beider Verfahren aufgehoben werden. Dieser hybride Algorithmus durchsucht effizient lokale Regionen mit Backpropagation, der globale Lösungsraum wird durch genetische Algorithmen analysiert und auch lokale Optima können wieder verlassen werden. Analog zur Natur wird die Optimierung neuronaler Netze durch einen hybriden genetischen Algorithmus in 2 Phasen unterteilt. Die Groboptimierung der Struktur neuronaler Netze durch Evolution und die Feinoptimierung der Gewichte durch Lernen. InitialisierungstechnikenDie Geschwindigkeit der Konvergenz vieler Lernverfahren, inklusive des detailliert behandelten Backpropagation-Lernverfahrens, hängt maßgeblich von der Initialisierung der Gewichte und Schwellwerte ab. Die bereits angesprochene Initialisierung der Verbindungsgewichte mit Zufallszahlen im Intervall [-1; 1] oder [-0.5; 0.5] stellt ein gutes Verfahren dar, um die Geschwindigkeit positiv zu beeinflussen. Um die Konvergenz weiter zu beschleunigen, können einige Anpassungen vorgenommen werden. Die dafür eingesetzten Initialisierungstechniken werden in diesem Abschnitt detailliert erörtert. Gleichverteilte ZufallszahlenEine triviale Technik, um ein neuronales Netz zu initialisieren besteht darin alle Verbindungsgewichte und Schwellwerte von einem Zufallszahlengenerator innerhalb eines vorgegebenen Intervalls setzen zu lassen. Diese Technik, auch “Hard Range Randomization” genannt, weist allen Objekten automatisch generierte Zufallszahlen zu.  Das Resultat ist ein flacher Graph. Umso mehr Zufallszahlen generiert werden, umso flacher sollte der Graph werden. Das Histgramm zeigt eine gleichmäßige Verteilung über das gesamte Spektrum. Die Güte des Zufallszahlengenerators bestimmt die Flachheit. Normalverteilte ZufallszahlenDie Verteilung der Verbindungsgewichte innerhalb von trainierten Netzen hat dazu geführt, dass vermehrt normalverteilte Zufallszahlen für die Initialisierung von künstlichen neuronalen Netzen verwendet wurden. Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) beschreibt die Verteilung einer Zufallsgröße X, bei der die graphische Darstellung der Wahrscheinlichkeitsdichte (f (x) = φ) die Form einer Glockenkurve (Normalverteilungskurve) besitzt.  Normalverteilte Zufallszahlen werden in den Ingenieurswissenschaften häufig verwendet. Für ihre Generierung kommt sehr oft die seit 1958 bekannte Box-Muller Transformation zum Einsatz. Siehe dazu auch Zufallszahlengeneratoren mit Gamma und Mersenne Twister. /// <summary> /// Compute a Gaussian random number. /// </summary> /// <param name="m">The mean.</param> /// <param name="s">The standard deviation.</param> /// <returns>The random number.</returns> public double BoxMuller(double m, double s) { double x1, x2, w, y1; // Use value from previous call if (_useLast) { y1 = _y2; _useLast = false; } else { do { x1 = 2.0d * NextDouble() - 1.0d; // NextDouble() is uniform in 0..1 x2 = 2.0d * NextDouble() - 1.0d; w = x1 * x1 + x2 * x2; } while (w >= 1.0d); w = Math.Sqrt((-2.0d * Math.Log(w)) / w); y1 = x1 * w; _y2 = x2 * w; _useLast = true; } return (m + y1 * s); } Nguyen-Widrow ZufallszahlenEine weitere Initialisierungstechnik wurde im Jahre 1990 von Derrick Nguyen und Bernard Widrow in ihrem Dokument "Improving the Learning Speed of 2-Layer Neural Networks by Choosing Initial Values of the Adaptive Weights" vorgestellt. Diese Technik ist bis heute eine sehr effektive Methode, um neuronale Netze zu initialisieren.  Stückweise ähnelt der Graph von Nguyen-Widrow der Normalverteilung. Innerhalb des Graphen sind ansteigende Höhen zu erkennen, die dann wieder an den Rändern stark abfallen. Es ist weiterhin zu erkennen, dass die Zufallsvariablen gestaucht wurden und im niedrigen Bereich um den Nullwert versammelt sind. Der Graph wurde für ein neuronales Netz mit vier Schichten (600, 400, 150, 40) und einem Intervall [-1; 1] für die Zufallsvariablen erstellt. Um eine Nguyen-Widrow Initialisierung zu realisieren, muss das künstliche neuronale Netz zunächst mit gleichmäßig verteilten Zufallszahlen initialisiert werden. Danach wird ein Wert β, wie folgt berechnet: .png) Die Variable H repräsentiert die Anzahl der verdeckten Neuronen im neuronalen Netzwerk, während die Variable N die Anzahl an Eingabeneuronen darstellt. Anschließend wird die euklidische Norm für alle Gewichte in einer Schicht berechnet. .png) Sobald β und die normalisierten Werte berechnet wurden, können die im ersten Schritt gesetzten Zufallszahlen angepasst werden. Die nachfolgende Formel zeigt, wie die Gewichte verändert werden. .png) Dieselbe Formel wird verwendet, um die Schwellwerte anzupassen. Sobald die Gewichte und Schwellwerte angepasst sind, kann das neuronale Netz trainiert werden. Die Initialisierung mit Nguyen-Widrow setzt voraus das mindestens eine verdeckte Schicht im neuronalen Netz präsent ist. Fan-In Weight ZufallszahlenDie sogenannte “Fan-In Weight Randomization” wurde von Simon Haykin in seinem Buch “Neural Networks - A Comprehensive Foundation” vorgestellt. Diese Technik ist ebenfalls effektiv, erreicht aber nicht die Qualität der Nguyen-Widrow Zufallszahlen.  Die Gewichte berechnen sich nach der folgenden Formel:  Zunächst wird der Bereich festgelegt, in welchem die Zufallszahlen für die Gewichte erzeugt werden sollen. Mit der Variable r wird die Anzahl der Neuronen in der aktuellen Schicht angegeben. Die Variable E steht für eine generierte Zufallszahl zwischen -1 und 1. Vorwärtsgerichtete neuronale NetzwerkeAlle vorwärtsgerichteten neuronalen Netze (engl. feedforward neural network) bestehen aus mehreren Schichten von Neuronen, mindestens jedoch aus einer Eingabe- und einer Ausgabeschicht. Eine oder mehrere innere Schichten können dazwischen liegen. Das wesentliche Merkmal von vorwärtsgerichteten neuronalen Netzen liegt darin das nur Neuronen verschiedener Schichten miteinander verknüpft sind und die Verbindungen nur in Richtung Ausgabeschicht bestehen. Vorwärtsgerichtete neuronale Netze werden stets überwacht mithilfe von Fehler-Rückmeldung trainiert. Das PerzeptronDas einfache Perzeptron ist ein vereinfachtes vorwärtsgerichtetes künstliches neuronales Netz ohne innere Schicht, das zuerst von Frank Rosenblatt 1958 vorgestellt wurde. Es wird durch ein simplifiziertes Backpropagation-Verfahren trainiert. Als Motivation für das Perzeptron diente das menschliche Auge, in dem eine Weiterleitung von Informationen vom Auge zum Gehirn stattfindet. Die Informationen werden von der Eingabeschicht über nicht weiter trainierbare Verbindungen mit festen Gewichten an die Darstellungsschicht übermittelt. Danach erfolgt eine Informationsverarbeitung über veränderliche Gewichte zur Ausgabeschicht. In Abbildung 6 ist eine Prinzipdarstellung dargestellt. Ein optisches Muster wird den verarbeitenden Einheiten der Darstellungsschicht übergeben, die anschließend die Informationen an die Ausgabe-Neuronen weiterreichen.  Dem Perzeptron wurde in den 60er-Jahren von Minsky und Papert nur eine eingeschränkte Leistungsfähigkeit nachgewiesen. Daraus zog man fälschlicherweise den Schluss künstliche neuronale Netze wären prinzipiell wenig zur Lösung der sich in der KI ergebenden Probleme geeignet. Mehrlagige Perzeptrons sind jedoch theoretisch in der Lage jede berechenbare Funktion zu realisieren. Pseudocode der Delta-RegelDie Delta-Regel für neuronale Netze mit nur einer trainierbaren Schicht lässt sich relativ einfach in Pseudocode ausdrücken. Zunächst werden alle Muster an die Eingabeschicht des Perzeptron gelegt. Anschließend wird die Ausgabe berechnet und für jedes Neuron die berechnete Ausgabe mit dem optimalen Wert verglichen. Besteht eine Abweichung, passt die Regel den Gewichtsfaktor entsprechend der Lernrate an.
FUNCTION Delta-Rule
REPEAT
FOR m := 1 TO Number of patterns DO
Set pattern to the input layer;
Calculate output values;
FOR j := 1 TO Number of output-neurons DO
IF teachoutputj ≠ outputj THEN
FOR i := 1 TO Number of input-neurons DO
wij = wij + learnrate * outputi * (teachoutputj - outputj);
END IF
END FOR
END FOR
Test all patterns;
UNTIL Result reached;
END Delta-Rule
Die Verbindungen zwischen Neuronen können als Punkte im n-dimensionalen Raum aufgefasst werden. Damit die berechneten Werte konvergieren können, müssen die Muster linear separierbar sein. Eine lineare Separierbarkeit ist dann sichergestellt, wenn zwei Relationen (Mengen aus n-Tupeln) in einer Hyperebene ℝ2, mithilfe einer Geraden in zwei voneinander trennbare Relationen aufgeteilt werden können. So ist es möglich ein einfaches Perzeptron mit zwei Eingabewerten und einem einzigen Ausgabeneuron zur Darstellung der logischen Operatoren AND, OR und NOT zu nutzen. Marvin Minsky und Seymour Papert wiesen jedoch 1969 nach, dass ein einlagiges Perzeptron den XOR-Operator nicht auflösen kann, da dieser nicht linear separierbar ist. Um eine XOR-Funktion nachbilden zu können ist ein mehrlagiges Perzeptron, d.h. ein Perzeptron mit mindestens einer inneren Schicht, erforderlich. Die Delta-Regel muss dann durch den verallgemeinerten Backpropagation-Algorithmus ersetzt werden. Mehrschichtige NetzeEin Perzeptron mit nur einer Eingabe- und Ausgabeschicht eignet sich für einfache Abbildungen, kann aber viele Problemstellungen nicht nachbilden. Aus diesem Grunde bestehen die meisten neuronalen Netze aus mehreren Schichten. Mehrschichtige Netze besitzen neben der Ausgabeschicht auch verdeckte Schichten (engl. hidden layer), deren Ausgabe außerhalb des Netzes nicht sichtbar sind. Verdeckte Schichten verbessern die Abstraktion solcher Netze. So kann erst das mehrschichtige Perzeptron das XOR-Problem lösen.  Netze mit einer oder mehreren verdeckten Schichten lassen sich nicht mit der Delta-Regel trainieren, sondern müssen mit dem Backpropagation-Algorithmus trainiert werden. In einem vorwärtsgerichteten Netz mit mindestens einer inneren Schicht von Neuronen sind mehrere Verbindungsschichten zu trainieren. Deshalb spricht man bei mehrschichtigen Netzen auch von Backpropagation-Netzen. Pseudocode des Backpropagation-AlgorithmusBeim Backpropagation-Algorithmus wird das Fehlersignal eines Neurons einer inneren Schicht mithilfe der Fehlesignale aller nachfolgenden Zellen und der zugehörigen Verbindungsgewichte bestimmt. Aufgrunddessen müssen zunächst die Fehlersignale der Ausgabe-Neuronen bestimmt werden, dann können die Fehlersignale der Neuronen der „letzten“ inneren Schicht berechnet werden, danach der „vorletzten“ Schicht und so weiter bis zur ersten inneren Schicht. Der Fehler wird von der Ausgabeschicht zur ersten inneren Schicht zurück geleitet. Daraus leitet sich die englische Bezeichnung Backpropagation (engl. Rückpropagierung) ab.
PROCEDURE Backpropagation
nCycles := 0;
REPEAT
error := 0;
nCycles := nCycles + 1;
FOR i := 1 TO Number of patterns DO
Set pattern i to the layer;
FOR j := 1 TO Number of output-neurons DO
Calculate output value oj;
Calculate error value fj := tj - oj;
Calculate error signal fsigj := oj * (1 - oj) * fj;
error := error + fj2;
END FOR
FOR s := Output layer - 1 DOWNTO First layer DO
FOR k := 1 TO Number of neuronal layers DO
fsum := 0;
FOR m := 1 TO Number of neuronal layer(s+1) DO
fsum := fsum + wkm * fsig(s+1)m;
END FOR
fsigsk := osk * (1 - osk) * fsum;
FOR m := 1 TO Number of neuronal layer(s+1) DO
wkm := wkm + learnrate * osk * fsig(s+1)m;
END FOR
END FOR
END FOR
END FOR
UNTIL error < Tolerable error OR Maximum cycles reached;
END Backpropagation
Entwicklung von Dekodier-NetzenEinfache Perzeptrons sind in der Lage direkte lineare Zuordnungen zu erlernen. Sie eignen sich deshalb sehr gut dazu binäre Darstellungen zu kodieren und zu dekodieren. In der folgenden Darstellung wird das Eingabemuster 0101 an die Eingabeschicht gereicht. Die Ausgabe-Neuronen erzeugen daraufhin die Ausgabe 001111111111.  Mithilfe der bisherigen Erkenntnisse wird nun ein Decoder-Perceptron in der Programmiersprache C# realisiert, mit dessen Hilfe eine Umrechnung vom binären Stellensystem in das dezimale Stellensystem stattfindet. Wir beginnen mit der Erstellung der Eingabeschicht. Dazu wird eine kleine Klasse für die Eingabe-Neuronen implementiert. using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace NeuralNetwork { public class InputNeuron { public InputNeuron() { Input = false; } // Auto-Impl Properties for trivial get and set public bool Input { get; set; } } } Die Eingabeschicht lässt nur boolesche Werte zu. Für die Verbindungen zwischen der Ein- und Ausgabeschicht des Perzeptrons wird eine Klasse using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace NeuralNetwork { public class Synapse { public Synapse(InputNeuron from) { Weight = 0.0; _from = from; } public InputNeuron From { get { return _from; } } public double Weight { get; set; } private InputNeuron _from; } } Der nächste Schritt ist die Programmierung der Ausgabeschicht. Die Ausgabe-Neuronen können mehrere Verbindungen besitzen. Die Verbindungen werden mithilfe der Synapsen in einer generischen Liste gespeichert. using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace NeuralNetwork { public class OutputNeuron { public OutputNeuron() { _threshold = 0.5; } public bool GetOutput() { double net = 0.0; for (int i = 0; i < _synapses.Count; i++) { net = net + _synapses[i].Weight * Convert.ToDouble(_synapses[i].From.Input); } // Fire, if we got over the threshold return (net > _threshold); } public void AddSynapse(Synapse s) { _synapses.Add(s); } public Synapse GetSynapse(int i) { return _synapses[i]; } public int GetSynapseSize() { return _synapses.Count; } private List<Synapse> _synapses = new List<Synapse>(); private double _threshold; } } Da ein Ausgabe-Neuron nur dann „feuert“, wenn der Eingabewert einen bestimmten Schwellwert überschreitet, wird die Ausgabe über die Eingabe aller Neuronen gewichtet aufsummiert. Der Schwellwert lässt sich über den Konstruktor setzen. Die bereitgestellten Objekte lassen sich nun in der Klasse Die Trainingsmuster sind binär in einem /// <summary> /// Does the net training based on the Delta-Rule. /// </summary> public void DeltaRule() { // For every teaching pattern, do... for(int p = 0; p < _patterns.Count; p++) { // Set the pattern to the input layer for(int i = 0; i < IN; i++) { _inputNeurons[i].Input = _patterns[p].Get(i); } // Calculate output of the output neurons CalculateOutput(); // For every output neuron, compare with pattern and adjust // weights if necessary for(int j = 0; j < OUT; j++) { if (_patterns[p].Get(j + IN) != NetOutput[j]) { for(int i = 0; i < _outputNeurons[j].getSynapseSize(); i++) { Synapse synapse = _outputNeurons[j].getSynapse(i); synapse.Weight = synapse.Weight + _learnRate * Convert.ToDouble(synapse.From.Input) * (Convert.ToDouble(_patterns[p].Get(j + IN)) - Convert.ToDouble(NetOutput[j])); } } } } } Training eines 4-15-PerzeptronUm das Netz testen zu können, wird nun ein Hauptprogramm implementiert. Das Dekodier-Netzwerk soll eine 4-stellige Binärzahl in eine Dezimalzahl dekodieren können. Dazu wird das 4-15-Perzeptron mit 4 Eingabe-Neuronen und 15 Ausgabe-Neuronen ausgestattet. Insgesamt sind 15 Ausgabe-Neuronen (N - 1) erforderlich, um 4 Bit vollständig dekodieren zu können. using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Windows; using System.Windows.Controls; using System.Windows.Data; using System.Windows.Documents; using System.Windows.Input; using System.Windows.Media; using System.Windows.Media.Imaging; using System.Windows.Navigation; using System.Windows.Shapes; using System.ComponentModel; using System.Windows.Threading; using System.Collections; namespace NeuralNetwork { /// <summary> /// Interaction logic for MainWindow.xaml /// </summary> public partial class MainWindow : Window, INotifyPropertyChanged { public MainWindow() { InitializeComponent(); labelWindowTitle.Content = "A " + INPUT + "-to-" + OUTPUT + "-Perceptron: Binary to Decimal"; this.DataContext = this; // Bind all user interface to this class DecimalNumber = _decimal = 4; labelBit0.Content = "0"; labelBit1.Content = "0"; labelBit2.Content = "1"; labelBit3.Content = "0"; _bits = new BitArray(BitConverter.GetBytes(_decimal)); _perceptron = new Perceptron(INPUT, OUTPUT, 0.05); _perceptron.Initialize(); // Add patterns _perceptron.SetPattern("0000", "000000000000000"); _perceptron.SetPattern("0001", "000000000000001"); _perceptron.SetPattern("0010", "000000000000011"); _perceptron.SetPattern("0011", "000000000000111"); _perceptron.SetPattern("0100", "000000000001111"); _perceptron.SetPattern("0101", "000000000011111"); _perceptron.SetPattern("0110", "000000000111111"); _perceptron.SetPattern("0111", "000000001111111"); _perceptron.SetPattern("1000", "000000011111111"); _perceptron.SetPattern("1001", "000000111111111"); _perceptron.SetPattern("1010", "000001111111111"); _perceptron.SetPattern("1011", "000011111111111"); _perceptron.SetPattern("1100", "000111111111111"); _perceptron.SetPattern("1101", "001111111111111"); _perceptron.SetPattern("1110", "011111111111111"); _perceptron.SetPattern("1111", "111111111111111"); } public void CalcPat() { int[] result = _perceptron.CalcDecimal(); for(int i = 0; i < 4; i++) { if (result[i] > 0) _bits[i] = true; else _bits[i] = false; } DecimalNumber = _decimal = result[4]; ShowOutput(); // Print curr output } // ... } Die grafische Benutzeroberfläche stellt mehrere Optionen zur Verfügung.  Mit dem Eingabemuster 0100 beginnend wird das Netz in 7 Lernschritten für die Dezimalwerte { 4, 0, 3, 5, 7, 15, 2 } trainiert. Diese reichen aus, damit das Netz auch alle anderen binären Eingabemuster richtig dekodieren kann. Nach Abschluss der Lernschritte können über den Netzstatus die Verbindungsgewichte angezeigt werden. Die Verbindungsgewichte lassen sich mit dem Menüpunkt "Table" abrufen. Diese zeigen die aktuelle Gewichte zwischen den vier Eingabe-Neuronen und den jeweiligen fünfzehn Ausgabe-Neuronen an.  Jede Zeile steht dabei für ein Eingabe-Neuron. Optische Zeichenerkennung (OCR)Einfache Dekodiernetze mit einlagigen Perzeptronen mögen bereits interessant sein, schöpfen aber das Potential von künstlichen neuronalen Netzen bei weitem nicht aus. Künstliche neuronale Netze sind dank der Fähigkeit zur Mustererkennung eine ideale Möglichkeit der automatischen Texterkennung, oft auch als OCR (optische Zeichenerkennung, englisch: optical character recognition) bezeichnet. Die optische Zeichenerkennung bezeichnet die automatisierte Texterkennung innerhalb von Bildern. Der Vorgang dieser Mustererkennung beginnt mit einer globalen Strukturerkennung, wobei zuerst die Grafiken separiert, daraufhin die Textseiten, dann die Zeilen und letzten Endes die einzelnen Zeichen betrachtet werden. In den Anfängen der optischen Zeichenerkennung vor vielen Jahren, gab es speziell für diesen Zweck entwickelte Schriftarten, vor allem zum einheitlichen Bedrucken von Scheckkarten, welche dann nicht mehr durch einen Menschen gelesen werden mussten, sondern von einer Maschine eingelesen werden konnten. Diese Schriftarten waren so gestaltet, dass die einzelnen Zeichen von einem OCR-Lesegerät schnell und ohne großen Rechenaufwand unterschieden werden konnten. Heutzutage ist es aber möglich, nahezu alle handelsüblichen Schriftarten und teilweise auch sehr leserliche Handschriften zu erkennen, letzteres ist vor allem in der Postbranche von Bedeutung. Die optische Zeichenerkennung von Handschriften erweist sich aber auch heute noch als problematisch. Davon unberührt ist die Technik heute soweit fortgeschritten, dass nicht nur Zeichen, sondern auch Zusammenhänge erkannt werden können. Diese Technik, auch als IRC (intelligente Zeichenerkennung, englisch: intelligent character recognition) bekannt, betrachtet nicht nur das einzelne Symbol, sondern auch den Kontext um es herum. So kann es, falls „8aum“ eingelesen wird, die „8“ in ein „B“ korrigieren. Diese Fähigkeit ist einer der Gründe, warum OCR/ICR-Systeme eine derart hohe Bedeutung haben. In diesem Abschnitt soll ein umfassendes OCR-Programm mit WPF (Windows Presentation Foundation) entwickelt werden, mit dem beliebige Zeichen erkannt werden können, auch handschriftlich gezeichnete Buchstaben. Die Grundlage bildet ein künstliches neuronales Netz, basierend auf dem vorgestellten Backpropagation-Algorithmus. Dazu wird eine leistungsfähige und unabhängig einsetzbare Bibliothek für neuronale Netze in C# entworfen. Vor der Implementierung werden zunächst alle theoretischen Aspekte, die für die Realisierung der Bilderkennung unabdingbar sind, erörtert. Datenaufbereitung mithilfe der BildverarbeitungKünstliche neuronale Netze verarbeiten in der Regel nur eindimensionale Eingaben und reagieren sehr unberechenbar auf stark variierende Daten. Bilder sind allerdings zweidimensionale Objekte und liegen in der Regel in keiner normierten Form vor. Ein Bild kann den Buchstaben "A" enthalten, aber in verschiedenen Schriftgrößen, Schriftarten, Schriftfarben oder sogar an verschiedenen Positionen im Bild. Trotz dieser Unterschiede ist das menschliche Gehirn in der Lage sich über diese Varianzen hinwegzusetzen und erkennt auch dann noch den Buchstaben "A", wenn dieser um 45° Grad gedreht worden ist.  Was für das Gehirn scheinbar einfach möglich ist, stellt für den Computer ein großes Problem dar. Bevor ein KNN zur Erkennung von Zeichen in Bildern eingesetzt werden kann, müssen die Bilddaten in eine eindeutige Form konvertiert werden, um dann der Eingabeschicht des künstlichen neuronalen Netzes zugeführt werden zu können. Dieser Schritt ist von großer Bedeutung für die Qualität der Zeichenerkennung und erfordert daher eine sorgfältige Planung. Die Bildverarbeitung bildet die Grundlage für die Vorbereitung der Bilddaten. Sie stellt weitergehende Bearbeitungsprozeduren zur Extraktion von Information aus den Ursprungsdaten wie Bewegungsbestimmung, Bildsegmentierung, Bilderkennung und Mustererkennung zur Verfügung. Die Bildverarbeitung wird heute in nahezu allen Wissenschafts- und Ingenieursdisziplinen eingesetzt und umfasst ein breites Spektrum von Techniken. Die zentralen Objekte der Bildverarbeitung sind die Bilder, die heute vorwiegend als Raster- oder Vektorgrafik vorliegen. RastergrafikEine Rastergrafik, auch Pixelgrafik (englisch Raster graphics image, Digital image, Bitmap oder Pixmap), ist eine Form der Beschreibung eines Bildes in Form von computerlesbaren Daten. Rastergrafiken bestehen aus einer rasterförmigen Anordnung von so genannten Pixeln (Bildpunkten), denen jeweils eine Farbe zugeordnet ist. Die Hauptmerkmale einer Rastergrafik sind daher die Bildgröße (Breite und Höhe gemessen in Pixeln, umgangssprachlich auch Bildauflösung genannt) sowie die Farbtiefe. VektorgrafikIm Gegensatz zu Rastergrafiken basieren Vektorgrafiken nicht auf einem Pixelraster, in dem jedem Bildpunkt ein Farbwert zugeordnet ist, sondern auf einer Bildbeschreibung, die die Objekte, aus denen das Bild aufgebaut ist, exakt definiert. So kann beispielsweise ein Kreis in einer Vektorgrafik über Lage des Mittelpunktes, Radius, Linienstärke und Farbe vollständig beschrieben werden; nur diese Parameter werden gespeichert. Im Vergleich zu Rastergrafiken lassen sich Vektorgrafiken daher oft mit deutlich geringerem Platzbedarf speichern. Eines der wesentlichen Merkmale und Vorteile gegenüber der Rastergrafik ist die stufenlose und verlustfreie Skalierbarkeit. Letztenendes wird aber jede Grafik gerastert und auf dem Bildschirm mit einer endlichen Punktmenge dargestellt, da jeder Bildschirm und Monitor nur eine begrenzte Auflösung bereit stellen kann. Auch das menschliche Auge besitzt mit 1 mm auf 3–6 Meter eine maximale Auflösung.  Erkennen von SymbolenDer Prozess der Bildanalyse zur Erkennung von Zeichensymbolen durch konsequente Untersuchung der Bildpixel ist der Kernpunkt für die Eingabeaufbereitung für das neuronale Netz. Abhängig vor der Anforderung an das OCR-Programm ist dieser Teil durchaus anspruchsvoll. Symbole werden in einem Bild basierend auf der Farbe der individuellen Pixel erkannt. Ein Farbbild wird in der Regel im RGB-Farbraum dargestellt. Ein RGB-Farbraum ist ein additiver Farbraum, der alle Farbwahrnehmungen durch das additive Mischen dreier Grundfarben (Rot, Grün und Blau) nachbildet. Dieser Farbraum basiert auf der Dreifarbentheorie. Das gesamte Farbsehen des Menschen ist durch drei Zapfentypen geprägt, die das Licht in drei unterschiedlichen Wellenlängen wahrnehmen können. Ein Bildpunkt ist nach dem RGB-Farbraum durch drei Anteile eindeutig definierbar. Diese Anteile werden als RGB(Rot, Grün und Blau) ausgeschrieben. So beschreibt das Tupel RGB(0, 0, 0) die Farbe Schwarz, während RGB(255, 255, 255) für ein weißes Pixel steht. Transparente Bilder erhalten als vierten Wert zusätzlich noch einen Alpha-Wert, der die Transparenz festlegt. Für die Erkennung von Buchstaben ist der Farbwert von untergeordneter Bedeutung. Ob ein Buchstabe schwarz ist oder blau ändert an seiner Semantik nichts. Deshalb besteht der erste Schritt bei der Bildaufbereitung und Erkennung von Symbolen darin, die Farbwerte zu eleminieren. Dazu wird ein beliebiges Bild in ein 8-Bit Graustufenbild konvertiert. Für die Arbeit mit Bildobjekten in WPF mit C# wird eine Klasse entworfen, die sich /// <summary> /// Converts a bitmap image to a new bitmap source with a new pixel format, /// like Gray8 or Rgb24. /// </summary> /// <param name="bitmapImage">The bitmap image.</param> /// <param name="pixelFormat">A pixel format from the PixelFormats class.</param> /// <returns>Returns a new converted bitmap.</returns> public static FormatConvertedBitmap ConvertImage(BitmapImage bitmapImage, PixelFormat pixelFormat) { // Convert the BitmapSource to a new format. // Use the BitmapImage created above as the source for a new BitmapSource object // which is set to a gray scale format using the FormatConvertedBitmap BitmapSource. // Note: New BitmapSource does not cache. It is always pulled when required. FormatConvertedBitmap formatConvertedBitmap = new FormatConvertedBitmap(); // BitmapSource objects like FormatConvertedBitmap can only have their properties // changed within a BeginInit/EndInit block. formatConvertedBitmap.BeginInit(); // Use the BitmapSource object defined above as the source for this new // BitmapSource (chain the BitmapSource objects together). formatConvertedBitmap.Source = bitmapImage; // Set the new format. formatConvertedBitmap.DestinationFormat = pixelFormat; formatConvertedBitmap.EndInit(); return formatConvertedBitmap; } Um den Schwierigkeitsgrad im Abschnitt Bildverarbeitung nicht übermäßig zu strapazieren, wird sich die Bildanalyse auf ein einzelnes Zeichen beschränken. Eine aufwendige Objektextraktion samt Segmentierung und Zuordnung mehrerer Zeichen fällt dadurch weg. Für das neuronale Netz spielt es keine Rolle, wieviele einzelne Zeichen diesem Netz zugeführt werden. Bei Bedarf kann zu einem späteren Zeitpunkt eine aufwendigere Objektextraktion von mehreren Symbolen implementiert werden. ObjektextraktionEin Symbol in einem Bild zu extrahieren ist am leichtesten, wenn das Bild leer ist bzw. sich keine weiteren Symbole auf dem Blatt befinden. Auch das menschliche Auge erkennt ein einzelnes Symbol auf einem leeren weißen Blatt leichter, als wenn dieses zwischen vielen Bildobjekten "versteckt" ist. Um ein Symbol auf einem leeren Blatt zu finden, wird das leere Blatt durchsucht und sobald ein Bildpunkt gefunden wurde, der vom Hintergrund abweicht, kann das Objekt weiterverfolgt und extrahiert werden. Dieser Vorgang ist nachfolgend abgebildet:  Um das gefundene Objekt wird ein Rechteck gezogen, dass das Objekt vollständig einrahmt. Die Klasse /// <summary> /// Segments a byte pixelated image. Depending on the level, all /// higher rows and columns are cropped. This method will create a /// rectangle around the segmented object. /// <code> /// Example: Image data with level=255: /// /// 255, 255, 255, 255, 255, 255, 255, 255, /// 255, 255, 255, 255, 255, 55, 255, 255, 255, 255, 255, 55, 255 /// 255, 255, 4, 8, 255, 15, 117, 255, 4, 8, 255, 15, 117, /// 255, 255, 9, 11, 255, 7, 55, 255, => 9, 11, 255, 7, 55, /// 255, 255, 5, 255, 255, 0, 25, 255, 5, 255, 255, 0, 25, /// 255, 255, 14, 2, 255, 3, 1, 255, 14, 2, 255, 3, 1 /// 255, 255, 255, 255, 255, 255, 255, 255 /// </code> /// </summary> /// <param name="pixels">A byte pixelated image.</param> /// <param name="stride">The stride (width) of the pixelated image.</param> /// <param name="level">The upper bound, which determines when a row/col gets cropped.</param> /// <param name="newWidth">The new width of the cropped bitmap.</param> /// <param name="newHeight">The new height of the cropped bitmap.</param> /// <exception cref="ArgumentOutOfRangeException">If arguments are invalid.</exception> /// <exception cref="NotSupportedException">If PixelFormat is not supported.</exception> /// <returns>The new cropped matrix in a linear array.</returns> public static byte[] RectangleExtraction(byte[] pixels, int stride, int level, PixelFormat pixelFormat, out int newWidth, out int newHeight) { if (pixels.Length < 1 || stride < 1) { throw new ArgumentOutOfRangeException(); } if (pixelFormat != PixelFormats.Gray8) { throw new NotSupportedException(); } int columns = stride; int rows = pixels.Length / stride; // Create a matrix[rows, columns] byte[,] matrix = To2dArray(pixels, columns); int yMin = -1, yMax = -1, xMin = -1, xMax = -1; // Compute the boundaries for (int i = 0; i < rows; i++) { if (Enumerable.Range(0, columns - 1).Any(j => matrix[i, j] < level)) { yMin = i; break; } } for (int i = rows - 1; i >= 0; i--) { if (Enumerable.Range(0, columns - 1).Any(j => matrix[i, j] < level)) { yMax = i; break; } } for (int i = 0; i < columns; i++) { if (Enumerable.Range(0, rows - 1).Any(j => matrix[j, i] < level)) { xMin = i; break; } } for (int i = columns - 1; i >= 0; i--) { if (Enumerable.Range(0, rows - 1).Any(j => matrix[j, i] < level)) { xMax = i; break; } } byte[,] subMatrix = null; // Check if we have a valid rectangle if (yMin == -1 || yMax == -1 || xMin == -1 || xMax == -1) { subMatrix = new byte[0, 0]; } else { subMatrix = Sub2dArray(matrix, yMin, yMax, xMin, xMax); } newHeight = subMatrix.GetLength(0); newWidth = subMatrix.GetLength(1); return To1dArray(subMatrix); } Der Algorithmus kann folgendermaßen beschrieben werden.
Abbildung des Symbols auf eine BildmatrixNeuronale Netze haben eine feste Eingabeschicht mit n Neuronen, weshalb auch das extrahierte Symbol in n Bildpunkte gerastert werden muss. Der Buchstabe "A" kann bei einer großen Darstellung aus vielen hunderten Bildpunkten bestehen. Dagegen hat ein kleines "A" vielleicht nur ein paar Dutzend Pixel. Es liegt auf der Hand dass das extrahierte Objekt normiert werden muss, damit es dieselbe Größe aufweist, wie die Eingabeschicht des künstlichen neuronalen Netzes. Der nächste Schritt der Datenaufbereitung besteht deshalb darin das Symbol in eine zweidimensionale Matrix zu konvertieren, deren Länge der Anzahl an Eingabeneuronen entspricht. Umso höher die Auflösung ist, umso mehr Details kann das neuronale Netz später unterscheiden. Allerdings sind bei einem Bild mit nur 100x150 Bildpunkten bereits 15000 Eingabeneuronen erforderlich. Mit jeder Verdoppelung der Bildzeilen und -spalten steigt diese Zahl im Quadrat an und erreicht bald astronomische Dimensionen. Das hat erhebliche Auswirkungen auf die Rechenzeit, so dass ein Kompromiss gefunden werden muss aus Leistung und Geschwindigkeit. In diesem Artikel wird für die Eingabematrix ein Wert von 44x55 Bildpunkten ausgewählt. Damit sind bereits 2420 Eingabeneuronen für die Erkennung notwendig. Um unterschiedlich große Zeichen an die vom neuronalen Netz festgelegten Eingabebedingungen anzupassen, wird das extrahierte rechteckige Bild nun skaliert. Dazu wird die Bildauflösung der Rastergrafik geändert. Das heißt, dass aus einer vorgegebenen Rastergrafik ein neues Bild mit einer höheren beziehungsweise niedrigeren Anzahl von Bildpunkten (Pixeln) erzeugt wird. Das .NET Framework stellt hierfür ebenfalls Methoden bereit, mit denen eine Bitmap skaliert werden kann. Die Grundlage für die Skalierung bildet die Koordinatentransformation im 2D-Vektorraum.  .NET stellt unter WPF für alle Koordinatentransformationen mit der Klasse Matrix eine 3x3 große affine Transformationsmatrix zur Verfügung, mit der eine Skalierung, Rotation, Scherung und Translation von Bildpunkten durchgeführt werden kann. Um die beiden Skalierfaktoren Sx und Sy zu ermitteln, muss lediglich die gewünschte Bildweite, durch die alte dividiert werden. Die Methode /// <summary> /// Resizes a given bitmap to a new size. /// </summary> /// <param name="source">The original bitmap source.</param> /// <param name="width">The width of the new scaled bitmap.</param> /// <param name="height">The height of the new scaled bitmap.</param> /// <returns>A new scaled bitmap.</returns> public static BitmapFrame Resize(BitmapSource source, double width, double height) { // Using ScaleTransform is also possible Matrix matrix = new Matrix(width / source.Width, 0, 0, height / source.Height, 0, 0); Transform scale = new MatrixTransform(matrix); TransformedBitmap tbBitmap = new TransformedBitmap(source, scale); return BitmapFrame.Create(tbBitmap); } Die Skalierung eines Objekts innerhalb der Bildmatrix kann mit Verlusten verbunden sein, falls die Zielmatrix zu klein ausfällt, um alle Strukturen eindeutig abzubilden oder das neue Seitenverhältnis eine Interpolation der Pixel erforderlich macht. Die Veränderung der Bildmatrix mitsamt Objekt kann nachfolgend betrachtet werden. Dasselbe Zeichen wird in zwei unterschiedlichen Rastergrößen dargestellt. Aufgrund des gleich bleibenden Seitenverhältnisses kommt es zu keinen Verlusten und es ist auch keine Interpolation der Bildpunkte notwendig.  Die Größenänderung mit dem Ziel die Bildpunkte an die Netzeingabe anzupassen, stellt den letzten Schritt bei der Bildaufbereitung dar. Ab diesem Zeitpunkt können die Daten bereits dem neuronalen Netz zum Training oder zur Identifikation übergeben werden. Das Bild wird dazu in "ausgefalteter" Form an die Neuronen der Eingabeschicht angelegt.  Aufbereitung der FarbwerteUm die Musterkennung positiv zu unterstützen wird noch ein weiterer Schritt durchgeführt, nämlich die Erstellung eines Negativ von dem Bild. Bei einem Negativfilm sind alle Farben umgekehrt, beispielsweise ist bei Schwarz-Weiß-Negativfilmen Weiß schwarz und Schwarz weiß, die entsprechenden Grauwerte werden entsprechend umgesetzt. Bei einem 8-Bit Graustufenbild, kann ein Negativ einfach durch das Komplement, eine logische Negation jedes Bits, durchführt werden. /// <summary> /// Inverts pixels of an image into their negative. A negative image is a /// total inversion of a positive image, in which light areas appear dark /// and vice versa. /// </summary> /// <param name="pixels">A byte array to invert.</param> /// <param name="pixelFormat">The PixelFormat of the image, like Gray8.</param> /// <exception cref="NotSupportedException">If PixelFormat is not supported.</exception> public static void Negative(byte[] pixels, PixelFormat pixelFormat) { switch (pixelFormat.BitsPerPixel) { case 8: // We currently support only 8-bit greyscale pictures for (int i = 0; i < pixels.Length; i++) { pixels[i] = (byte)(~pixels[i]); } break; default: throw new NotSupportedException(); } } Durch das Negativ werden die dunklen Bildpixel der Zeichen hell dargestellt und erhalten damit höhere Graustufenwerte. Entwicklung einer .NET-Bibliothek für künstliche neuronale NetzeDie Erkennung von Schriftzeichen mithilfe von neuronalen Netzen setzt die Implementierung der vorgestellten Algorithmen voraus. Während die Delta-Regel sehr schnell in Code umzusetzen ist, erfordert der Backpropagation-Algorithmus etwas mehr Zeit. Da die optische Zeichenerkennung nur einen Einsatzbereich für künstliche neuronale Netze darstellt, macht es Sinn an dieser Stelle eine universell einsetzbare .NET-Bibliothek zu entwerfen. Für den Entwurf einer guten Bibliothek eignet sich die Modellierung mithilfe der UML (engl. Unified Modeling Language). Ziel beim Entwurf ist es, die Bibliothek leistungsfähig, universell einsetzbar, benutzerfreundlich und leicht erweiterbar zu gestalten. Letzter Punkt ist gerade für den Aspekt einer nachträglichen Implementierung von genetischen Algorithmen vorteilhaft. In diesem Kapitel wird eine .NET-Bibliothek für künstliche neuronale Netze in C# entworfen. Implementierung der AktivierungsfunktionenNeuronale Netze besitzen eine Aktivierungsfunktion, um bei einer bestimmten Eingabe den korrespondierenden Ausgabewert zu generieren. Aus diesem Grunde ist es sinnvoll zunächst mit der Implementierung der Aktivierungsfunktionen zu beginnen, da diese völlig unabhängig von allen anderen Modulen realisiert werden können. Nachfolgend sind die Klassendiagramme von fünf verschiedenen Aktivierungsfunktionen abgebildet. Alle leiten sich von der Schnittstelle  Die Schnittstelle /// <summary> /// A threshold function for a neural network. /// </summary> /// <remarks> /// <code> /// 1 /// f(x) = ------------------- beta > 0 /// 1 + e^(-beta * x) /// </code> /// </remarks> /// <param name="x">The input to the function.</param> /// <returns>The output from the function.</returns> public double F(double x) { return (1.0 / (1 + Math.Exp(-_beta * x))); } Implementierung der MusterklassenAlle Werte in der Bibliothek basieren auf einem 8-Byte großen  Die Schnittstelle Implementierung der Linearen AlgebraIm Kapitel über Hopfield-Netze und über Netzwerkarchitekturen kamen die Matrizen bereits zur Sprache. Vektoren und Matrizen sind ein Schlüsselkonzept der Linearen Algebra. Um Berechnungen in einem neuronalen Netz durchzuführen, sind Vektoren und Matrizen ideal geeignet. In einer Matrix zur Darstellung von Verbindungen können gleichzeitig auch die Verbindungsgewichte abgespeichert werden. Die Entwicklung einer entsprechenden Vektor- und Matrixklasse folgt den mathematischen Grundlagen. Zu den klassischen Berechnungen gehört das Skalarprodukt oder die Addition und Multiplikation von zwei Matrizen. Im Namensraum  Um die Berechnung zu vereinfachen und für den Aufrufer intuitiver zu gestalten, wurden alle wesentlichen arithmetischen Operatoren überladen. Im nachfolgenden Beispiel werden zwei Matrizen multipliziert.  double[,] a = { { 14, 9, 3 }, { 2, 11, 15 }, { 0, 12, 17 }, { 5, 2, 3 } }; double[,] b = { { 12, 25 }, { 9, 10 }, { 8, 5 } }; Matrix A = new Matrix(a); Matrix B = new Matrix(b); Matrix C = A * B; Console.WriteLine(C.ToString()); Da die Größe der Matrizen abhängig von der Anzahl der Verbindungen und Neuronen ist und diese Zahl bei großen neuronalen Netzen sehr hoch ausfallen kann, wurde in der Klasse Implementierung des NetzwerksMit den bisher implementierten Klassen wurde das wichtige Fundament für die gesamte Bibliothek gelegt. Der nächste Schritt besteht nun darin die neuronalen Netzwerkklassen zu entwerfen. Diese arbeiten unabhängig vom Algorithmus und stellen im Wesentlichen nur das neuronale Netz selbst dar. Dazu zählen die Schichten mit ihren Neuronen, sowie die Aktivierungsfunktion mitsamt den Gewichten und Schwellwerten. Das neuronale Netz wird aus Schichten, die aus Neuronen bestehen, zusammengesetzt. Dazu wird die Klasse  Jede Netzwerkschicht verfügt in der Regel über eine sogenannte LayerMatrix oder auch Schichtmatrix. Die LayerMatrix ist der Dreh- und Angelpunkt der Datendarstellung und -verarbeitung. Diese Matrix beschreibt sowohl die Zahl der Neuronen in der aktuellen Schicht, als auch die Zahl der Neuronen in der nachfolgenden Schicht, sowie alle Verbindungsgewichte und Schwellwerte. Demzufolge verfügt ein Netzwerk mit n Schichten über n-1 Matrizen. Die Ausgabeschicht ist die einzige Schicht, die über keine eigene LayerMatrix verfügt, da sie keine nachfolgende Schicht besitzt. Die Struktur der Schichtmatrix gestaltet sich wie folgt:  Um den prinzipiellen Aufbau des neuronalen Netzwerks mit Schichtmatrizen zu verstehen, ist es von Vorteil ein vollständiges Netzwerkbeispiel zu betrachten. Nachfolgend wird ein trainiertes XOR-Gatter, welches sich bekanntlich nicht mit einem zweilagigen Perzeptron realisieren lässt, in drei Schichten dargestellt. Die erste Schicht, auch Eingabeschicht genannt, besteht aus zwei Neuronen. Dazwischen befindet sich eine verdeckte Schicht (engl. Hidden Layer) mit insgesamt drei Neuronen. Die dritte Schicht stellt die Ausgabeschicht dar. Diese Ausgabeschicht besteht nur aus einem Neuron.  Die Ein- und Ausgabemuster der XOR-Funktion sind in der nachfolgenden Tabelle beschrieben: Wahrheitstabelle:
Das Netzwerk mit drei Schichten lässt sich mit insgesamt zwei Matrizen vollständig darstellen. Die Eingabeschicht besitzt die erste Matrix, die verdeckte Schicht die zweite Matrix. Nun lassen sich die beiden Matrizen des abgebildeten XOR-Gatters skizzieren.  Mit dem Prinzip der Schichtenmatrizen lässt sich ein vollständiges neuronales Netz beschreiben. Zum Ende dieses Abschnitts wird der Ausgabewert aus den oben dargestellten Werten berechnet. Als Aktivierungsfunktion wird die sigmoide Funktion mit β=1 verwendet.  Der Eingabevektor (1, 0, 1) stellt die Eingabe der XOR-Funktion dar, wobei der dritte Wert lediglich als Faktor für den Schwellwert (engl. bias, threshold) dient und mit diesem einfach multipliziert wird, ohne ihn zu verändern, da die 1 das neutrale Element der Multiplikation ist. Aus dem Eingabevektor und jedem Spaltenvektor der ersten Matrix wird das Skalarprodukt gebildet. Das Skalarprodukt realisiert die Netzeingabe netj = Σ wij * oj - θj indem es die Eingabe mit den Verbindungsgewichten multipliziert und die Ergebnisse zusammen mit dem Schwellwert addiert. Der positive oder negative Schwellwert verschiebt mathematisch die Aktivierungsfunktion auf der x-Achse nach links oder rechts. Es ist üblich, den Schwellwert in die Formel der Netzeingabe mit aufzunehmen. Das Resultat wird anschließend der sigmoiden Aktivierungsfunktion zugeführt, die die Ausgabe des jeweiligen Neurons berechnet. Die berechnete Ausgabe der drei Neuronen in der verdeckten Schicht dient nun wiederum als Eingabe für das Neuron der Ausgabeschicht. Dazu wird erneut der Eingabevektor gebildet, mit dem neutralen Element 1 am Ende für den Schwellwert. Aus dem Skalarprodukt und der Aktivierungsfunktion ergibt sich die endgültige Ausgabe des Netzwerks, nämlich 0,998. Das ist die erwartete Ausgabe für die XOR-Funktion bei der angelegten Eingabe (1, 0). Da als Aktivierungsfunktion die sigmoide, logistische Funktion verwendet wurde, erreicht die Ausgabe nie ganz den Wert 1, da die Aktivierungsfunktion eine Asymptote bei -1 und 1 besitzt. Implementierung des Backpropagation-AlgorithmusDas künstliche neuronale Netzwerk wurde im letzten Abschnitt komplettiert. Doch ohne ein Lernverfahren kann es nicht trainiert werden und ist damit nutzlos. In diesem Abschnitt soll deshalb ein Lernverfahren implementiert werden, das die Verbindungsgewichte und Schwellwerte der Schichtenmatrizen automatisch berechnet. Für mehrschichtige neuronale Netze wird der beschriebene Backpropagation-Algorithmus verwendet. Die Grundlage für den C#-Code bildet der bereits vorgestellte Pseudocode. Der Aufbau des Backpropagation basiert auf der Struktur des neuronalen Netzwerks. Jeder Netzwerkschicht wird eine Backpropagationschicht zugewiesen, die das Fehlersignal berechnet. Die Klasse  Neben der Hauptmethode ProgrammbeispielDie .NET-Bibliothek für künstliche neuronale Netze kann mit der Vervollständigung des Lernverfahrens endgültig genutzt werden. Als Programmbeispiel wird das beschriebene XOR-Gatter verwendet. Zu Beginn werden die Trainingsmuster für XOR erstellt. Nachdem ein neuronales Netz mit drei Schichten generiert wurde, kann das Netz mit dem Backpropagation-Algorithmus trainiert werden. Dazu wird die Eingabe zusammen mit der erwartenden Ausgabe und den beiden Parametern Alpha und Gamma an den Algorithmus übergeben. Neben dem tolerierbaren Fehler und der maximalen Iterationsanzahl, wird ein Ereignis gesetzt, das alle 100 Iterationen aufgerufen wird. In der Methode public class XOR { /// <summary> /// Create, train and use a neural network for XOR. /// </summary> /// <param name="args">Not used</param> static void Main(string[] args) { XOR xor = new XOR(); xor.Execute(); } public void Execute() { try { ISample sample0 = new StandardSample(new double[] { 0.0, 0.0 }, new double[] { 0.0 }); ISample sample1 = new StandardSample(new double[] { 0.0, 1.0 }, new double[] { 1.0 }); ISample sample2 = new StandardSample(new double[] { 1.0, 0.0 }, new double[] { 1.0 }); ISample sample3 = new StandardSample(new double[] { 1.0, 1.0 }, new double[] { 0.0 }); SampleSet sampleSet = new SampleSet(2, 1); sampleSet.Add(sample0); sampleSet.Add(sample1); sampleSet.Add(sample2); sampleSet.Add(sample3); int[] neuronLayers = { 2, 3, 1 }; INeuralNetwork network = new FeedforwardNeuralNetwork(neuronLayers); ILearningAlgorithm algorithm = new Backpropagation(network, sampleSet, 0.7, 0.9); algorithm.MaxIterations = 5000; algorithm.TolerableError = 0.001; algorithm.Interval = 100; algorithm.AlgorithmEvent += new EventHandler<AlgorithmEventArgs>(NeuralNetwork_IterationChanged); algorithm.Learn(); // Test the neural network Console.WriteLine("XOR with Artificial Neural Network:\n"); foreach (ISample sample in sampleSet.Samples) { double[] actual = network.ComputeOutput(sample.GetInput()); Console.WriteLine(sample.GetInput()[0] + ", " + sample.GetInput()[1] + ", actual=" + actual[0] + ", ideal=" + sample.GetOutput()[0]); } } catch (Exception e) { Console.WriteLine(e.Message); } Console.Read(); } public void NeuralNetwork_IterationChanged(object sender, AlgorithmEventArgs args) { Console.WriteLine("Event raised on iteration {0} with error {1}.", args.Iteration, args.Error); } } SchlussIn dem Artikel wurden die Möglichkeiten von künstlichen neuronalen Netzen und ihre Einschränkungen erörtert. Über ein einfaches Perzeptron, das in C# implementiert wurde, konnte ein Dekodierer entwickelt werden, der bereits nach wenigen Lernschritten Musterzuordnungen richtig erlernt und anschließend alle restlichen Dezimalwerte ebenfalls korrekt anzeigt. Mithilfe der vorgestellten .NET-Bibliothek können mithilfe des Backpropagation auch komplexe Aufgaben mit künstlichen neuronalen Netzen realisiert werden. Die Erkennung von CAPTCHA ist mit mehrlagigen Perzeptrons problemlos möglich. Dabei lassen sich überwachte Netze mithilfe von bekannten Bild-Werte-Paaren trainieren. Künstliche neuronale Netze der dritten Generation, sogenannte Spiking Neural Networks (SNN), arbeiten mit Differentialgleichungen höherer Ordnung zur Berechnung der Aktivierung und nutzen ebenfalls zeitliche Abhängigkeiten der Neuronen untereinander. Die Forschung auf dem Gebiet der künstlichen Intelligenz versucht in Zusammenarbeit mit der Hirnforschung die ersten Schritte zu einem sich selbstorganisierenden System zu gehen. Im Vergleich zu einem Computer, der aufgrund seiner Architektur ein rein logisch beschreibbares statisches System mit deterministischen Verhalten darstellt, ist das Gehirn ein dynamisches System mit kontinuierlichen, rauschbehafteten Rechenelementen und steht im Verdacht des indeterministischen Verhaltens. Das komplexe Verhalten resultiert durch Interaktion einfacher Elemente untereinander und mit der Außenwelt ohne externe Programmierung. Lediglich aus dem Zusammenspiel der Bausteine emergieren Aktivitätsmuster, die die eigentliche Gehirntätigkeit ausmachen. Moderne neuronale Netze versuchen diese Methodik umzusetzen. Weblinks
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Zuletzt aktualisiert am Montag, den 13. Januar 2014 um 22:20 Uhr |
| AUSWAHLMENÜ | ||||||||
|
 Wir suchen ständig neue Tutorials und Artikel! Habt ihr selbst schonmal einen Artikel verfasst und seid bereit dieses Wissen mit der Community zu teilen? Oder würdet ihr gerne einmal über ein Thema schreiben das euch besonders auf dem Herzen liegt? Dann habt ihr nun die Gelegenheit eure Arbeit zu veröffentlichen und den Ruhm dafür zu ernten. Schreibt uns einfach eine Nachricht mit dem Betreff „Community Articles“ und helft mit das Angebot an guten Artikeln zu vergrößern. Als Autor werdet ihr für den internen Bereich freigeschaltet und könnt dort eurer literarischen Ader freien Lauf lassen.
Wir suchen ständig neue Tutorials und Artikel! Habt ihr selbst schonmal einen Artikel verfasst und seid bereit dieses Wissen mit der Community zu teilen? Oder würdet ihr gerne einmal über ein Thema schreiben das euch besonders auf dem Herzen liegt? Dann habt ihr nun die Gelegenheit eure Arbeit zu veröffentlichen und den Ruhm dafür zu ernten. Schreibt uns einfach eine Nachricht mit dem Betreff „Community Articles“ und helft mit das Angebot an guten Artikeln zu vergrößern. Als Autor werdet ihr für den internen Bereich freigeschaltet und könnt dort eurer literarischen Ader freien Lauf lassen.
